
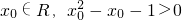 ”的否定¬P:“?x∈R,x2-x-1≤0”
”的否定¬P:“?x∈R,x2-x-1≤0”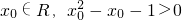 ”的否定¬P:“?x∈R,x2-x-1≤0”正确.
”的否定¬P:“?x∈R,x2-x-1≤0”正确.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2013届安徽怀远县包集中学高二下学期期中考试理科数学试卷(解析版) 题型:填空题
有下列命题:
①;到两个定点 距离的和等于定长的点的轨迹是椭圆;
距离的和等于定长的点的轨迹是椭圆;
②命题“若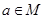 ,则
,则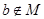 ”的逆否命题是:若
”的逆否命题是:若 ;
;
③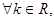 曲线
曲线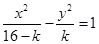 表示双曲线
表示双曲线
④设集合M = {x | 0< x ≤3},N = {x | 0< x ≤2},则“a∈M”是“a∈N”的充分而不必要条件则上述命题中真命题为 (填上序号)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年宁夏高三第一次模拟考试文科数学试卷 题型:选择题
有下列命题:
①设集合M = {x | 0< x ≤3},N = {x | 0< x ≤2},则“a∈M”是“a∈N”的充分而不必要条件;
②命题“若 ,则
,则 ”的逆否命题是:若
”的逆否命题是:若 ;
;
③若 是假命题,则
是假命题,则 都是假命题;
都是假命题;
④命题P:“ ”的否定
”的否定 :“
:“ ”
”
则上述命题中为真命题的是
A.①②③④ B.①③④ C.②④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com