
分析 (I)利用抛物线的定义,点M(2$\sqrt{3}$,m)到其焦点F的距离.求解p,点的坐标满足方程求m的值;
(Ⅱ)设A(x1,y1),B(x2,y2),利用平方差法,以及$\overrightarrow{OA}•\overrightarrow{OB}=6$,求出y2y1=-6,表示出三角形的面积,利用基本不等式求解△ABO面积的最小值.
解答 解:(Ⅰ)由抛物线定义可得$2\sqrt{3}+\frac{p}{2}=\frac{{9\sqrt{3}}}{4}$,解得$p=\frac{{\sqrt{3}}}{2}$,
∴所求抛物线方程为${y^2}=\sqrt{3}x$,
把M($2\sqrt{3}$,m)代入可解得$m=±\sqrt{6}$,…(4分)
(Ⅱ)设A(x1,y1),B(x2,y2),则$y_1^2=\sqrt{3}{x_1}$,$y_2^2=\sqrt{3}{x_2}$.
由$\overrightarrow{OA}•\overrightarrow{OB}=6$,得$\frac{y_1^2y_2^2}{3}+{y_1}{y_2}=6$,
又A,B在该抛物线上且位于x轴的两侧,故y2y1=-6.…(6分)
∵$cos∠AOB=\frac{{\overrightarrow{OA}•\overrightarrow{OB}}}{{|{\overrightarrow{OA}}|•|{\overrightarrow{OB}}|}}$,$sin∠AOB=\sqrt{1-{{(\frac{{\overrightarrow{OA}•\overrightarrow{OB}}}{{|{\overrightarrow{OA}}|•|{\overrightarrow{OB}}|}})}^2}}$
∴${S_{△ABO}}=\frac{1}{2}|{\overrightarrow{OA}}||{\overrightarrow{OB}}|sin∠AOB=\frac{1}{2}|{\overrightarrow{OA}}||{\overrightarrow{OB}}|\sqrt{1-{{(\frac{{\overrightarrow{OA}•\overrightarrow{OB}}}{{|{\overrightarrow{OA}}|•|{\overrightarrow{OB}}|}})}^2}}$…(8分)
=$\frac{1}{2}\sqrt{{{(|{\overrightarrow{OA}}||{\overrightarrow{OB}}|)}^2}-36}$=$\frac{1}{2}\sqrt{(\frac{y_1^4}{3}+y_1^2)(\frac{y_2^4}{3}+y_2^2)-36}$=$\frac{1}{2}\sqrt{12(y_1^2+\frac{36}{y_1^2}+12)}$=$\sqrt{3}|{y_1^{\;}+\frac{6}{{y_1^{\;}}}}|≥6\sqrt{2}$.
∴△ABO面积的最小值为$6\sqrt{2}$. …(12分)
点评 本题考查抛物线的方程的综合应用,直线与抛物线的位置关系,考查转化思想以及计算能力.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
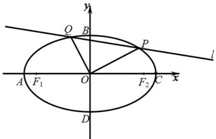 如图,在直角坐标系xOy中,椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点分别为F1,F2,左、右、上、下四个顶点分别为A,C,B,D,四边形F1BF2D的面积与四边形ABCD的面积的比值为$\frac{{\sqrt{6}}}{3}$.
如图,在直角坐标系xOy中,椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点分别为F1,F2,左、右、上、下四个顶点分别为A,C,B,D,四边形F1BF2D的面积与四边形ABCD的面积的比值为$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com