
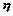 表示更换的面数,用
表示更换的面数,用 表示更换费用。
表示更换费用。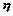 的分布
的分布 列,求
列,求 的数学期望。
的数学期望。 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源:不详 题型:解答题
 产品中只有一个合格产品的概率是多少?
产品中只有一个合格产品的概率是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 冲击“常识关”,乙冲击“创新关”,已知甲回答“常识关”中每道题正确的概率都为
冲击“常识关”,乙冲击“创新关”,已知甲回答“常识关”中每道题正确的概率都为 ,乙回答“创新关”中每道题正确的概率都为
,乙回答“创新关”中每道题正确的概率都为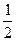 ,且两关之间互不影响,每道题回答正确与否相互独立.
,且两关之间互不影响,每道题回答正确与否相互独立. ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.35 | B.0.30 | C.0.25 | D.0.20 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 . 若可通过的信息量
. 若可通过的信息量 ≥6,则可保证信息通畅.
≥6,则可保证信息通畅. 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 的分布列分别为:
的分布列分别为: | 8 | 9 | 10 |
| P | 0.3 | 0.5 | a |
 | 8 | 9 | 10 |
| P | 0.2 | 0.3 | b |
 )确定a、b的值,并求两人各进行一次射击,都射中10环的概率;
)确定a、b的值,并求两人各进行一次射击,都射中10环的概率; 的分布列及期望,并求结束时射击轮次超过2次的概率。
的分布列及期望,并求结束时射击轮次超过2次的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
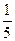 ,已知袋中红球有3个,则袋中共有球的个数为
,已知袋中红球有3个,则袋中共有球的个数为 | A.4 | B.5 | C.6 | D.7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com