
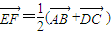 .
.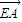 +
+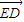 =
= ,
, +
+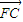 =
=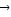 ,利用平面向量加法的三角形法则,我们易将向量
,利用平面向量加法的三角形法则,我们易将向量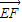 分别表示为
分别表示为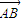 +
+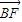 +
+ 和
和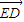 +
+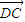 +
+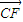 的形式,两式相加后,易得到结论.
的形式,两式相加后,易得到结论. ,由向量加法的平行四边形法则,我们易将向量
,由向量加法的平行四边形法则,我们易将向量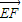 表示为
表示为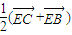 ,然后再利用向量加法的三角形法则,即可得到结论.
,然后再利用向量加法的三角形法则,即可得到结论. 证法一:如图,
证法一:如图,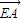 +
+ =
= ,
, +
+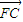 =
=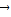 ,
,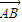 +
+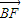 +
+ +
+ =
=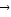 ,
,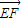 =
= +
+ +
+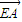 ①
① =
=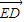 +
+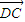 +
+ ②
②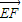 =
= +
+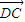 +
+ +
+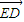 +
+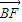 +
+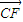 =
= +
+ .
.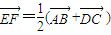 .
.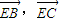 ,
,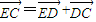 ,
,

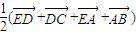
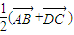 .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
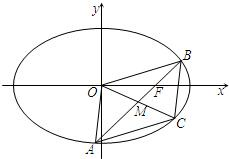 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| ||
| 7 |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省合肥市高三第一次教学质量检测文科数学试卷(解析版) 题型:填空题
有下列命题:
①已知 是平面内两个非零向量,则平面内任一向量
是平面内两个非零向量,则平面内任一向量 都可表示为
都可表示为 ,其中
,其中 ;
;
②对任意平面四边形ABCD,点E、F分别为AB、CD的中点,则 ;
;
③直线 的一个方向向量为
的一个方向向量为 ;
;
④已知 与
与 夹角为
夹角为 ,且
,且 ·
· =
= ,则|
,则| -
- |的最小值为
|的最小值为 ;
;
⑤ 是(
是( ·
· )·
)· =
= ·(
·( ·
· )的充分条件;
)的充分条件;
其中正确的是 (写出所有正确命题的编号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com