
(12分)已知数列 ,
, 满足
满足 ,
,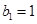 ,且
,且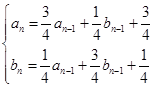 (
(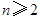 )
)
(Ⅰ)求数列 ,
, 的通项公式.
的通项公式.
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(Ⅰ)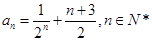 ,
,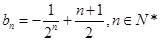 ;(Ⅱ)
;(Ⅱ)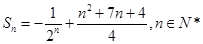 .
.
解析试题分析:(Ⅰ)本题的已知条件中, 、
、 在所满足的关系式中相互交叉表达,显然无法从现有已知条件中直接求出
在所满足的关系式中相互交叉表达,显然无法从现有已知条件中直接求出 、
、 的通项公式,所以必须通过构造新的数列来间接求解,再根据关系式中的系数特征可以看出,两个条件相加、减后得到的结果分别构成等差、等比数列,从而找到本题的突破口,接下来只需通过加、减消元即可得出所求;(Ⅱ)在(Ⅰ)中求得
的通项公式,所以必须通过构造新的数列来间接求解,再根据关系式中的系数特征可以看出,两个条件相加、减后得到的结果分别构成等差、等比数列,从而找到本题的突破口,接下来只需通过加、减消元即可得出所求;(Ⅱ)在(Ⅰ)中求得 的通项公式的基础上,只需借助相关前
的通项公式的基础上,只需借助相关前 项求和的恰当方法,不难得出所求.
项求和的恰当方法,不难得出所求.
试题解析:(Ⅰ)由题设得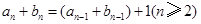 ,
,
可令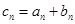 ,则
,则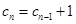 (
(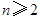 ),即
),即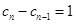 ,
,
所以 是首项为
是首项为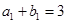 ,公差为1的等差数列,通项公式为
,公差为1的等差数列,通项公式为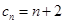 ,
,
由题设得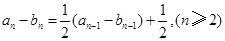 ,
,
可令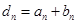 ,则
,则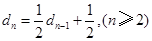 ,即
,即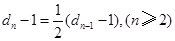 ,
,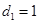 ,
,
所以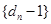 是首项为
是首项为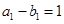 ,公比为
,公比为 的等比数列,通项公式为
的等比数列,通项公式为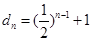 .
.
综上所述,可得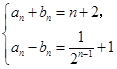 解之得:
解之得: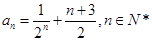 ;
;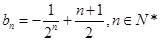 ;
;
(Ⅱ)由(Ⅰ)知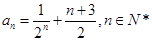 ,
,
显然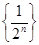 是首项为
是首项为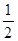 ,公比为
,公比为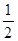 的等比数列,
的等比数列,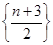 是首项为2,公差为
是首项为2,公差为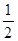 的等差数列,
的等差数列,
所以数列 的前
的前 和
和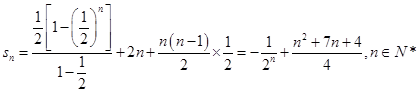 .
.
考点:数列的构造思想;等差、等比数列的定义、通项公式及前 项和;分组求和的方法;方程思想和发散思维.
项和;分组求和的方法;方程思想和发散思维.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:解答题
(本小题满分13分)在四棱锥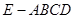 中,底面
中,底面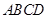 是正方形,
是正方形, 与
与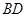 交于点
交于点 ,
,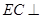 底面
底面 ,
, 为
为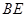 的中点.
的中点. 
(Ⅰ)求证: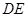 ∥平面
∥平面 ;
;
(Ⅱ)求证: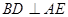 ;
;
(Ⅲ)若 在线段
在线段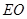 上是否存在点
上是否存在点 ,使
,使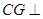 平面
平面 ?
?
若存在,求出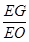 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com