
分析 (1)根据奇函数的性质即可求出a,设x∈[0,4],-x∈[-4,0],易求f(-x),根据奇函数性质可得f(x)与f(-x)的关系;
(2)分离参数,构造函数,求出函数的最值问题得以解决.
解答 解:(1)f(x)是定义在[-4,4]上的奇函数,
∴f(0)=1+a=0,
∴a=-1,
∵$f(x)=\frac{1}{4^x}-\frac{1}{3^x}$,
设x∈[0,4],
∴-x∈[-4,0],
∴$f(x)=-f(-x)=-[{\frac{1}{{{4^{-x}}}}-\frac{1}{{{3^{-x}}}}}]={3^x}-{4^x}$,
∴x∈[0,4]时,f(x)=3x-4x
(2)∵x∈[-2,-1],$f(x)≤\frac{m}{2^x}-\frac{1}{{{3^{x-1}}}}$,
即$\frac{1}{4^x}-\frac{1}{3^x}≤\frac{m}{2^x}-\frac{1}{{{3^{x-1}}}}$
即$\frac{1}{4^x}+\frac{2}{3^x}≤\frac{m}{2^x}$x∈[-2,-1]时恒成立,
∵2x>0,
∴${({\frac{1}{2}})^x}+2•{({\frac{2}{3}})^x}≤m$,
∵$g(x)={({\frac{1}{2}})^x}+2•{({\frac{2}{3}})^x}$在R上单调递减,
∴x∈[-2,-1]时,$g(x)={({\frac{1}{2}})^x}+2•{({\frac{2}{3}})^x}$的最大值为$g(-2)={({\frac{1}{2}})^{-2}}+2•{({\frac{2}{3}})^{-2}}=\frac{17}{2}$,
∴$m≥\frac{17}{2}$.
点评 本题考查函数的奇偶性及其应用,不等式恒成立的问题,考查学生解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 某工厂随机抽取部分工人调查其上班路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),若上班路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某工厂随机抽取部分工人调查其上班路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),若上班路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2${\;}^{\frac{5}{6}}$ | B. | 2${\;}^{\frac{3}{2}}$ | C. | 2${\;}^{\frac{1}{6}}$ | D. | 2${\;}^{(\frac{1}{2})^{\frac{1}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,A是函数f(x)=2x的图象上的动点,过点A作直线平行于x轴,交函数g(x)=2x+2的图象于点B,若函数f(x)=2x的图象上存在点C使得△ABC为等边三角形,则称A为函数f(x)=2x上的好位置点.函数f(x)=2x上的好位置点的个数为( )
如图所示,A是函数f(x)=2x的图象上的动点,过点A作直线平行于x轴,交函数g(x)=2x+2的图象于点B,若函数f(x)=2x的图象上存在点C使得△ABC为等边三角形,则称A为函数f(x)=2x上的好位置点.函数f(x)=2x上的好位置点的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
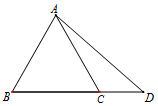 如图,△ABC是等边三角形,点D在边BC的延长线上,且BC=2CD,AD=$\sqrt{7}$.
如图,△ABC是等边三角形,点D在边BC的延长线上,且BC=2CD,AD=$\sqrt{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com