
分析 (Ⅰ)若a=1,则A={x|1<x≤6},由此能求出A∪B.
(Ⅱ)由a>0,得A={x|$\frac{1}{a}<x≤\frac{6}{a}$}.再由A∩B=∅,得$\frac{1}{a}≥2$,由此能求出实数a的取值集合.
解答 解:(Ⅰ)若a=1,则A={x|1<x≤6},
所以A∪B={x|-$\frac{1}{2}<x≤6$}.…(4分);
(Ⅱ)因为a>0,所以A={x|$\frac{1}{a}<x≤\frac{6}{a}$}.
由于A∩B=∅,所以$\frac{1}{a}≥2$,即0<a$≤\frac{1}{2}$.
综上所述:实数a的取值集合$({0,\frac{1}{2}}]$.…(10分).
点评 本题考查并集的求法,考查实数的取值范围的求法,是基础题,解题时要认真审题,注意不等式性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{3}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
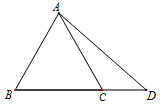 如图,△ABC是等边三角形,点D在边BC的延长线上,且BC=2CD,AD=$\sqrt{7}$.
如图,△ABC是等边三角形,点D在边BC的延长线上,且BC=2CD,AD=$\sqrt{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com