
分析 (1)由三角形内角和定理表示出$\frac{A+C}{2}$,利用诱导公式化简求出B的度数,再利用余弦定理求出c的值即可;
(2)f(A)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的三角函数,由A的范围求出f(A)的范围即可.
解答 解:(1)在△ABC中,A+C=π-B,
∴cos$\frac{A+C}{2}$=cos$\frac{π-B}{2}$=sin$\frac{B}{2}$=$\frac{1}{2}$,
∴$\frac{B}{2}$=$\frac{π}{6}$,即B=$\frac{π}{3}$,
由余弦定理:b2=a2+c2-2accosB,得c2-3c+2=0,
解得:c=1或c=2;
(2)f(A)=$\frac{\sqrt{3}}{2}$sinA-$\frac{1-cosA}{2}$+$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sinA+$\frac{1}{2}$cosA=sin(A+$\frac{π}{6}$),
由(1)A+C=π-B=$\frac{2π}{3}$,得到A∈(0,$\frac{2π}{3}$),
∴A+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),
∴sin(A+$\frac{π}{6}$)∈($\frac{1}{2}$,1],
则f(A)的范围是($\frac{1}{2}$,1].
点评 此题考查了余弦定理,以及三角函数中的恒等变换应用,熟练掌握定理及公式是解本题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | 0 | C. | -$\frac{3}{2}$ 或 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂随机抽取部分工人调查其上班路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),若上班路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某工厂随机抽取部分工人调查其上班路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),若上班路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
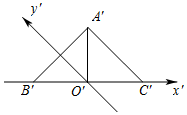 用斜二侧法画水平放置的△ABC的直观图,得到如图所示等腰直角△A′B′C′.已知点O′是斜边B′C′的中点,且A′O′=1,则△ABC的BC边上的高为( )
用斜二侧法画水平放置的△ABC的直观图,得到如图所示等腰直角△A′B′C′.已知点O′是斜边B′C′的中点,且A′O′=1,则△ABC的BC边上的高为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2${\;}^{\frac{5}{6}}$ | B. | 2${\;}^{\frac{3}{2}}$ | C. | 2${\;}^{\frac{1}{6}}$ | D. | 2${\;}^{(\frac{1}{2})^{\frac{1}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
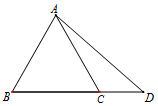 如图,△ABC是等边三角形,点D在边BC的延长线上,且BC=2CD,AD=$\sqrt{7}$.
如图,△ABC是等边三角形,点D在边BC的延长线上,且BC=2CD,AD=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com