
| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
分析 根据向量的减法的运算法则将向量进行化简,然后两边平方,设$\overrightarrow{AB}$•$\overrightarrow{AO}$=m,整理可得4t2-2tm-(4-2m)≥0恒成立,再由不等式恒成立思想,运用判别式小于等于0,解不等式即可.
解答 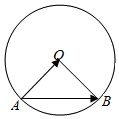 解:∵|$\overrightarrow{AB}$-t$\overrightarrow{AO}$|≥|$\overrightarrow{BO}$|,
解:∵|$\overrightarrow{AB}$-t$\overrightarrow{AO}$|≥|$\overrightarrow{BO}$|,
∴|$\overrightarrow{AB}$-t$\overrightarrow{AO}$|≥|$\overrightarrow{AO}$-$\overrightarrow{AB}$|,
两边平方可得:
$\overrightarrow{AB}$2-2t$\overrightarrow{AB}$•$\overrightarrow{AO}$+t2$\overrightarrow{AO}$2≥$\overrightarrow{AO}$2-2$\overrightarrow{AO}$•$\overrightarrow{AB}$+$\overrightarrow{AB}$2,
设$\overrightarrow{AB}$•$\overrightarrow{AO}$=m,则有:4t2-2tm-(4-2m)≥0恒成立,
则有判别式△=4m2+16(4-2m)≤0,
即m2-8m+16≤0,
化简可得(m-4)2≤0,即m=4,
即有$\overrightarrow{AB}$•$\overrightarrow{AO}$=4,
故选:B
点评 本题考查平面向量的运用,考查平方法的运用,考查向量的平方即为模的平方,考查二次不等式恒成立的求法,注意运用判别式小于等于0,考查运算能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
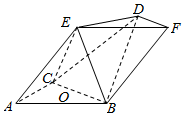 如图,多面体ABCDEF中,四边形ABEF是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.
如图,多面体ABCDEF中,四边形ABEF是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com