
分析 (I)利用向量数量积运算性质即可得出.
(II)利用向量夹角公式即可得出.
解答 解:(Ⅰ)∵$|{\overrightarrow a{+}\overrightarrow b}|{=}|{\overrightarrow a}|$.
∴${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{a}}^{2}$,即$2\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=0…(2分)
∴2(7x-4)+50=0,解得x=-3…(5分)
(Ⅱ)设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,$\overrightarrow{a}$=(-3,4),$\overrightarrow{b}$=(7,-1),∴$\overrightarrow{a}•\overrightarrow{b}$=-21-4=-25,…(6分)
且$|\overrightarrow{a}|$=$\sqrt{{3}^{2}+{4}^{2}}$=5,$|\overrightarrow{b}|$=5$\sqrt{2}$…(8分),
∴$cosθ=\frac{{{a}•{b}}}{{|{a}||{b}|}}=\frac{-25}{{5×5\sqrt{2}}}=-\frac{{\sqrt{2}}}{2}$.…(9分)
∵θ∈[0,π],∴$θ=\frac{3π}{4}$,即a,b夹角为$\frac{3π}{4}$.…(10分)
点评 本题考查了向量数量积的运算性质、向量夹角公式,考查了推理能力与计算能力,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
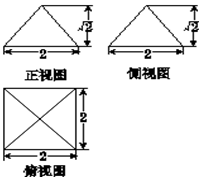 如图所示,某几何体的正视图、侧视图均为等腰三角形,俯视图是正方形,则该几何体的体积是( )
如图所示,某几何体的正视图、侧视图均为等腰三角形,俯视图是正方形,则该几何体的体积是( )| A. | 2 | B. | 4 | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{{8\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [1,3] | C. | [2,4] | D. | [3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数段 | [0~80) | [80~100) | [100~120) | [120~140) | [140~150] |
| 人数 | 300 | 130 | 180 | 220 | 170 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{2}{3},2)$ | B. | $(\frac{2}{3},2]$ | C. | $[1,\frac{4}{3}]$ | D. | $(1,\frac{4}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com