
| A. | (0,$\frac{\sqrt{2}}{2}$]∪[4,+∞) | B. | [$\frac{\sqrt{2}}{2}$,1)∪(1,4] | C. | ($\frac{\sqrt{2}}{2}$,1)∪(1,4) | D. | (0,$\frac{\sqrt{2}}{2}$)∪(4,+∞) |
分析 作函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)与函数y=ax(a>0,a≠1)的图象,利用数形结合的方法求解即可.
解答 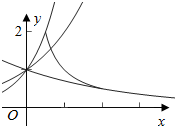 解:作函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)与函数y=ax(a>0,a≠1)的图象,
解:作函数y=$\frac{1}{x}$($\frac{1}{2}$≤x≤2)与函数y=ax(a>0,a≠1)的图象,
结合图象可知,当0<a<1时,a2≥$\frac{1}{2}$,
解得$\frac{\sqrt{2}}{2}$≤a<1;
当a>1时,${a}^{\frac{1}{2}}$≤2,
解得1<a≤4.
综上可得,$\frac{\sqrt{2}}{2}$≤a<1或1<a≤4.
故选:B.
点评 本题考查了学生的作图与应用图象的能力,同时考查了指数函数的性质,属于中档题.


科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(文)试卷(解析版) 题型:解答题
已知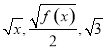 (x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(1)求数列{an}的第n+1项;
(2)若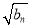 是
是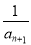 ,
,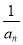 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:选择题
在等差数列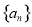 中,已知
中,已知 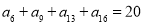 ,则S21等于( )
,则S21等于( )
A.100 B.105 C.200 D.0
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7米/秒 | B. | 6米/秒 | C. | 5米/秒 | D. | 8米/秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6x-y-18=0 | B. | 8x-y-24=0 | C. | 5x-2y-15=0 | D. | 8x-3y-24=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com