解:(Ⅰ)∵对任意x∈R都有f(x)+f(-x)=4对任意x∈R恒成立,
∴f(0)=2,即m=1…(2分)
(Ⅱ)∵m=1,故f(x)=-x
3+3x+2,
∴f′(x)=-3x
2+3,令-3x
2+3=0得:x
1=-1,x
2=1…(5分)
若-1<x<1,f′(x)>0,若x>1,f′(x)<0,当x=1或x=-1,f′(x)=0,
∴f(x)=-x3+3x+2在(-1,1)上单调递增,在(1,+∞)上单调递减;
∴f(x)
极大值=f(1)=4,
又f(-1)=1-3+2=0,
f(3)=-27+9+2=-16.
∴函数f(x)在[-1,3]上的最大值为4;…(8分)
(Ⅲ)由(Ⅰ)得m=1,∴f(x)=-x
3+3x+2=(1+x)
2(2-x),…(10分)
由(Ⅱ)知,当x∈[0,3]时,(1+x)
2(2-x)≤4,

…(12分)
当a,b,c∈[0,+∞)且a+b+c=3时,0≤a≤3,0≤b≤3,0≤c≤3,
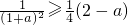
,
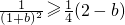
,
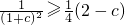
,
∴
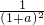
+
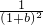
+
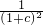
≥
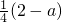
+
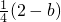
+
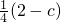
=

[6-(a+b+c)]=

…(14分)
分析:(Ⅰ)可令x=0,即可求得m的值;
(Ⅱ)m=1,f(x)=-x
3+3x+2,f′(x)=-3x
2+3,先求函数f(x)在[-1,3]上的极值,再求其在端点的函数值,其中最大的就是所求;
(Ⅲ)由(Ⅰ)得m=1,f(x)=-x
3+3x+2=(1+x)
2(2-x),(Ⅱ)知,当x∈[0,3]时,(1+x)
2(2-x)≤4,于是

,当a,b,c∈[0,+∞)且a+b+c=3时,0≤a≤3,0≤b≤3,0≤c≤3,
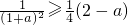
,
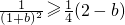
,
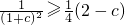
,利用同向不等式相加即可.
点评:本题考查不等式的证明,重点考查利用导数求函数的闭区间上的最值及不等式的性质证明,难点在于(Ⅰ)(Ⅱ)(Ⅲ)结论的高度结合,特别是(1+x)
2(2-x)≤4到

的转化,属于难题.

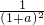 +
+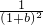 +
+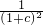
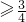 .
. …(12分)
…(12分)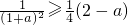 ,
,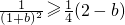 ,
,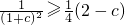 ,
,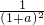 +
+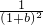 +
+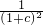 ≥
≥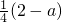 +
+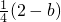 +
+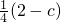 =
= [6-(a+b+c)]=
[6-(a+b+c)]= …(14分)
…(14分) ,当a,b,c∈[0,+∞)且a+b+c=3时,0≤a≤3,0≤b≤3,0≤c≤3,
,当a,b,c∈[0,+∞)且a+b+c=3时,0≤a≤3,0≤b≤3,0≤c≤3,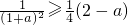 ,
,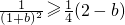 ,
,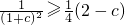 ,利用同向不等式相加即可.
,利用同向不等式相加即可. 的转化,属于难题.
的转化,属于难题. 
