练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】

    1. (2015·四川）如果函数f(x)=(m-2)x2+(n-8)x+1(m≥0， n≥0）在区间[, 2]上单调递减，则mn的最大值为（ ）


    A.16
    B.18
    C.25
    D.

    【答案】B
    【解析】m≠2时， 抛物线的对称轴为x=-, 据题意，当m>2时，-≥2即2m+n≤12， ∵≤≤6, ∴mn≤18, 由2m=n且2m+n=12得m=3, n=6, 当，m<2时， 抛物线开口向下， 根据题意， -≤即m+2n≤18， ∵≤≤9, ∴mn≤, 由2n=m且m+2n=18得m=9>2, 故应舍去使得mn取得最大值，应有m+2n=18(m<2,n>8), 所以mn=(18-2n)n<(18-2x8)x8=16, 所以最大值为18. 选B
    【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正方体中，点是棱上的一个动点，平面交棱于点．给出下列命题：

    ①存在点，使得//平面；

    ②对于任意的点，平面平面；

    ③存在点，使得平面；

    ④对于任意的点，四棱锥的体积均不变.

    其中正确命题的序号是______．（写出所有正确命题的序号）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设a,b,c是△ABC的三边,P: , Q:方程x2 +2ax+b2 = 0与方程x2 +2cx－b2 = 0有公共根. 则P是Q的_____.(填：充分不必要条件,必要而不充分条件,充要条件,既不充分也不必要条件)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）=xlnx﹣ax2+（2a﹣1）x，a∈R．
    （1）令g（x）=f′（x），求g（x）的单调区间；
    （2）已知f（x）在x=1处取得极大值，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

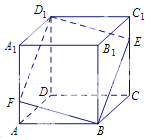
    【题目】如图，正方体ABCD—A1B1C1D1，

    则下列四个命题：

    ①P在直线BC1上运动时，三棱锥A—D1PC的体积不变；

    ②P在直线BC1上运动时，直线AP与平面ACD1所成角的大小不变；

    ③P在直线BC1上运动时，二面角P—AD1—C的大小不变；

    ④M是平面A1B1C1D1上到点D和C1距离相等的点，则M点的轨迹是过D1点的直线D1A1。

    其中真命题的编号是 。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过点、，并且直线： 平分圆.

    （Ⅰ）求圆的方程；

    （Ⅱ）若过点，且斜率为的直线与圆有两个不同的交点.

    （ⅰ）求实数的取值范围；

    （ⅱ）若，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax2﹣ax﹣1（a∈R）．
    （1）若对任意实数x，f（x）＜0恒成立，求实数a的取值范围；
    （2）当a＞0时，解关于x的不等式f（x）＜2x﹣3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在原点，焦点在轴上的椭圆过点，离心率为.

    （1）求椭圆的方程；

    （2）直线过椭圆的左焦点，且与椭圆交于两点，若的面积为，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，椭圆的左右顶点分别是，为直线上一点（点在轴的上方），直线与椭圆的另一个交点为，直线与椭圆的另一个交点为.

    （1）若的面积是的面积的，求直线的方程；

    （2）设直线与直线的斜率分别为，求证：为定值.

    查看答案和解析>>

    同步练习册答案