
【题目】数列{xn}满足x1=0,xn+1=﹣x2n+xn+c(n∈N*).
(Ⅰ)证明:{xn}是递减数列的充分必要条件是c<0;
(Ⅱ)求c的取值范围,使{xn}是递增数列.
【答案】解:(Ⅰ)当c<0时,xn+1=﹣x2n+xn+c<xn ,
∴{xn}是单调递减数列
充分条件
当{xn}是单调递减数列时
x1=0>x2=﹣x21+x1+c
∴c<0
综上{xn}是从递减数列的充分必要条件是c<0;
(Ⅱ)由(I)得,c≥0
①当c=0时,xn=x1=0,此时数列为常数列,不符合题意;
②当c>0时,x2=c>x1=0,x3=﹣c2+2c>x2=c
∴0<c<1![]()
![]()
0=x1≤xn< ![]() ,
, ![]() =﹣(xn+1﹣xn)(xn+1+xn﹣1),
=﹣(xn+1﹣xn)(xn+1+xn﹣1),
当0<c ![]() 时,
时, ![]() xn﹣xn+1+1>0xn+2﹣xn+1﹣1<0,xn+2﹣xn+1与xn+1﹣xn同号,
xn﹣xn+1+1>0xn+2﹣xn+1﹣1<0,xn+2﹣xn+1与xn+1﹣xn同号,
由x2﹣x1=c>0xn+1﹣xn>0xn+1>xn . ![]() =
= ![]()
![]() .
.
当c ![]() 时,存在N使xN
时,存在N使xN![]() xN+xN+1>1xN+2﹣xN+1与xN+1﹣xN异号,
xN+xN+1>1xN+2﹣xN+1与xN+1﹣xN异号,
与数列{xn}是从递减数列矛盾.
所以当0<c ![]() 时,数列{xn}是递增数列
时,数列{xn}是递增数列
【解析】(Ⅰ)通过证明必要条件与充分条件,推出{xn}是从递减数列的充分必要条件是c<0;(Ⅱ)由(I)得,c≥0,通过①当c=0时,②当c>0时,推出0<c<1,当c ![]() 时,证明xn+1>xn .
时,证明xn+1>xn . ![]() =
= ![]()
![]() .当c
.当c ![]() 时,说明数列{xn}是从递减数列矛盾.得到0<c
时,说明数列{xn}是从递减数列矛盾.得到0<c ![]() 时,数列{xn}是递增数列.
时,数列{xn}是递增数列.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在钝角△ABC中,∠A为钝角,令 ![]() =
= ![]() ,
, ![]() =
= ![]() ,若
,若 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R).现给出下面结论:
(x,y∈R).现给出下面结论:
①当x= ![]() 时,点D是△ABC的重心;
时,点D是△ABC的重心;
②记△ABD,△ACD的面积分别为S△ABD , S△ACD , 当x= ![]() 时,
时, ![]() ;
;
③若点D在△ABC内部(不含边界),则 ![]() 的取值范围是
的取值范围是 ![]() ;
;
④若 ![]() =λ
=λ ![]() ,其中点E在直线BC上,则当x=4,y=3时,λ=5.
,其中点E在直线BC上,则当x=4,y=3时,λ=5.
其中正确的有(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x+λ3﹣x(λ∈R).
(1)若f(x)为奇函数,求λ的值和此时不等式f(x)>1的解集;
(2)若不等式f(x)≤6对x∈[0,2]恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对新招聘的员工张某进行综合能力测试,共设置了A,B,C三个测试项目.假定张某通过项目A的概率为 ![]() ,通过项目B,C的概率均为a(0<a<1),且这三个测试项目能否通过相互独立.
,通过项目B,C的概率均为a(0<a<1),且这三个测试项目能否通过相互独立.
(1)用随机变量X表示张某在测试中通过的项目个数,求X的概率分布和数学期望E(X)(用a表示);
(2)若张某通过一个项目的概率最大,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,F为双曲线C:![]() ﹣
﹣![]() =1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
=1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
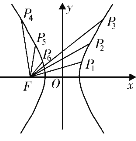
A. 9 B. 16 C. 18 D. 27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=![]() , AB=2,CD=3,M为PC上一点,PM=2MC.
, AB=2,CD=3,M为PC上一点,PM=2MC.
(Ⅰ)证明:BM∥平面PAD;
(Ⅱ)若AD=2,PD=3,求二面角D﹣MB﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“嫦娥奔月,举国欢庆”,据科学计算,运载“神六”的“长征二号”系列火箭,在点火第一秒钟通过的路程为2 km,以后每秒钟通过的路程都增加2 km,在达到离地面210 km的高度时,火箭与飞船分离,则这一过程大约需要的时间是______秒.
【答案】14
【解析】
设出每一秒钟的路程为一数列,由题意可知此数列为等差数列,然后根据等差数列的前n项和的公式表示出离地面的高度,让高度等于210列出关于n的方程,求出方程的解即可得到n的值.
设每一秒钟通过的路程依次为a1,a2,a3,…,an,
则数列{an}是首项a1=2,公差d=2的等差数列,
由求和公式有na1+![]() =210,即2n+n(n﹣1)=210,
=210,即2n+n(n﹣1)=210,
解得n=14,
故答案为:14
【点睛】
在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质是两种数列基本规律的深刻体现,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.
【题型】填空题
【结束】
16
【题目】已知直线l:![]() +
+![]() =1,M是直线l上的一个动点,过点M作x轴和y轴的垂线,垂足分别为A,B,点P是线段AB的靠近点A的一个三等分点,点P的轨迹方程为______.
=1,M是直线l上的一个动点,过点M作x轴和y轴的垂线,垂足分别为A,B,点P是线段AB的靠近点A的一个三等分点,点P的轨迹方程为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是_____________ .(填序号)
①棱柱的面中,至少有两个面互相平行;
②以直角三角形的一边为轴旋转所得的旋转体是圆锥;
③用一个平面去截圆锥,得到一个圆锥和一个圆台;
④有两个面平行,其余各面都是平行四边形的几何体叫棱柱;
⑤圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com