
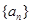 为等比数列,
为等比数列,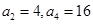 ,记
,记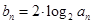 .
.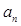 和
和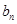 ;
;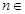
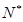 ,有
,有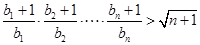 成立.
成立.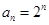 ,
,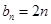 ;(2)详见解析.
;(2)详见解析.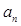 ,进而得
,进而得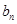 ;(2)对于与自然数有关的命题的证明可优先考虑用数学归纳法,用数学归纳法证题时,首先要掌握好数学归纳法证题的规范、完整的证题步骤,而真正的难点和重点是由假设来推导第
;(2)对于与自然数有关的命题的证明可优先考虑用数学归纳法,用数学归纳法证题时,首先要掌握好数学归纳法证题的规范、完整的证题步骤,而真正的难点和重点是由假设来推导第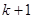 步,这里要充分地利用假设,若是对于恒等式的证明在利用了假设以后就很容易推导出第
步,这里要充分地利用假设,若是对于恒等式的证明在利用了假设以后就很容易推导出第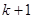 步,但是对于不等式的证明在利用了假设以后还不能一下子就推导出第
步,但是对于不等式的证明在利用了假设以后还不能一下子就推导出第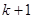 步,还需要对照目标进行适当的放缩处理才能推导出第
步,还需要对照目标进行适当的放缩处理才能推导出第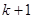 步,放缩处理是有难度,且需要技巧的,这需要在学习中去积累.
步,放缩处理是有难度,且需要技巧的,这需要在学习中去积累.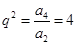 ,又
,又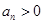 ,所以
,所以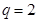 ,从而
,从而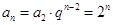 ,进而有
,进而有  . 4分
. 4分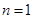 时,左边
时,左边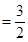 ,右边
,右边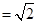 ,因为
,因为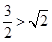 ,所以不等式成立. 5分
,所以不等式成立. 5分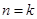 时,不等式成立,即
时,不等式成立,即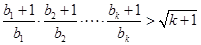 成立. 7分
成立. 7分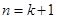 时,则左边
时,则左边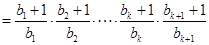
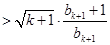
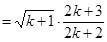
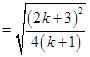
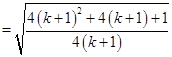
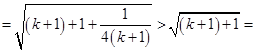 右边 12分
右边 12分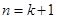 时,不等式也成立.
时,不等式也成立.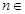
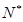 ,都有
,都有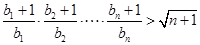 恒成立. 14分
恒成立. 14分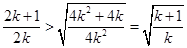 )
)

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源:不详 题型:解答题
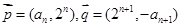 ,n∈N*,向量
,n∈N*,向量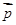 与
与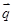 垂直,且a1=1.
垂直,且a1=1.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 1 |
| an |
| m |
| 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com