【题目】如图所示，四棱锥B-AEDC中，平面AEDC⊥平面ABC，F为BC的中点，P为BD的中点，且AE//DC，∠ACD=∠BAC=90°，DC=AC=AB=2AE
（1）证明：EP⊥平面BCD；
（2）若DC=2，求三棱锥E-BDF的体积.
寒假学与练系列答案科目：高中数学 来源： 题型：
【题目】设椭圆
（
）的右焦点为
，右顶点为
，已知
，其中
为原点，
为椭圆的离心率.
（Ⅰ）求椭圆的方程；
（Ⅱ）设过点的直线
与椭圆交于点
（不在
轴上），垂直于的直线与
交于点
，与
轴交于点
，若
，且
，求直线的斜率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校研究性学习小组从汽车市场上随机抽取
辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于
公里和
公里之间，将统计结果分成
组：
，
，
，
，
，绘制成如图所示的频率分布直方图.
（1）求直方图中
的值；
（2）求续驶里程在
的车辆数；
（3）若从续驶里程在的车辆中随机抽取
辆车，求其中恰有一辆车的续驶里程在内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高二年级800名学生参加了地理学科考试，现从中随机选取了40名学生的成绩作为样本，已知这40名学生的成绩全部在40分至100分之间，现将成绩按如下方式分成6组：第一组
；第二组
；……；第六组
，并据此绘制了如图所示的频率分布直方图．
（1）求每个学生的成绩被抽中的概率；
（2）估计这次考试地理成绩的平均分和中位数；
（3）估计这次地理考试全年级80分以上的人数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合M是满足下列性质的函数
的全体：在定义域
内存在
，使函数
成立；
（1）请给出一个的值，使函数
（2）函数
是否是集合M中的元素？若是，请求出所有组成的集合；若不是，请说明理由；
（3）设函数
,求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是
,且每题正确完成与否互不影响.
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算均值;
(2)试从两位考生正确完成题数的均值及至少正确完成2题的概率分析比较两位考生的实验操作能力.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.右图是以往公司对该产品的宣传费用
(单位：万元)和产品营业额
(单位：万元)的统计折线图.
(Ⅰ)根据折线图可以判断，可用线性回归模型拟合宣传费用与产品营业额的关系，请用相关系数加以说明；
(Ⅱ)建立产品营业额关于宣传费用的回归方程；
(Ⅲ)若某段时间内产品利润
与宣传费和营业额的关系为
应投入宣传费多少万元才能使利润最大，并求最大利润. (计算结果保留两位小数)
参考数据：
，
，
，
，
参考公式：相关系数
，回归方程
中斜率和截距的最小二乘法估计公式分别为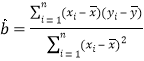
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某支教队有8名老师，现欲从中随机选出2名老师参加志愿活动，
（1）若规定选出的至少有一名女老师，则共有18种不同的需安排方案，试求该支教队男、女老师的人数；
（2）在（1）的条件下，记
为选出的2位老师中女老师的人数，写出的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
