练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．在正方体ABCD-A1B1C1D1中，AA1=3，点E在棱AB上，点F在棱C1D1上，且平面B1CF∥平面A1DE，若AE=1，则三棱锥B1-CC1F外接球的表面积为19π．

    分析 根据平面B1CF∥平面A1DE，得到C1F=AE=1，再求出三棱锥B1-CC1F外接球直径，问题得以解决．

    解答 解：当C1F=AE=1时，可得CF∥A1E，
    又A1D1∥B1C，且CF∩B1C=C，
    ∴平面B1CF∥平面A1DE，
    ∴三棱锥B1-CC1F外接球的直径为$\sqrt{{3}^{2}+{3}^{2}+{1}^{2}}$=$\sqrt{19}$，
    其表面积为（$\sqrt{19}$）2π=19π，
    故答案为：19π

    点评 本题主要考查了正方体和三棱锥的几何体的性质以及球的表面积公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．已知函数f（x）=$\left\{\begin{array}{l}{xlnx-2x，x＞0}\\{{x}^{2}+\frac{3}{2}x，x≤0}\end{array}\right.$的图象上有且仅有四个不同的点关于直线y=-1的对称点在y=kx-1的图象上，则实数k的取值范围是（$\frac{1}{2}$，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．给甲、乙、丙三人打电话，若打电话的顺序是任意的，则第一个打电话给丙的概率是（　　）
    A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

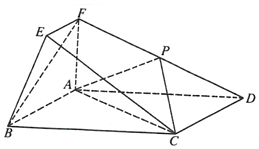    2．在如图所示的几何体中，四边形ABCD为矩形，直线AF⊥平面ABCD，EF∥AB，AD=2，AB=AF=2EF=1，点P在棱DF上．
    （1）求证：AD⊥BF；
    （2）若P是DF的中点，求异面直线BE与CP所成角的余弦值；
    （3）若$\overrightarrow{FP}=\frac{1}{3}\overrightarrow{FD}$，求二面角D-AP-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．通过随机询问110名性别不同的大学生是否爱好某处运动，得到如下的列联表：
    男女合计
    爱好402060
    不爱好203050
    合计6050110
    由卡方公式算得：K2≈7.8
    附表：
    P（K2≥k）0.0500.0100.001
    k3.8416.63510.828
    参照附表：得到的正确的结论是（　　）
    A．在犯错的概率不超过0.1%的前提下，认为“爱好该运动与性别无关”
    B．在犯错的概率不超过0.1%的前提下，认为“爱好该运动与性别有关”
    C．有99%以上的把握认为“爱好该运动与性别有关”
    D．有99%以上的把握认为“爱好该运动与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知A、B分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右顶点，P为双曲线上一点，且△ABP为等腰三角形，若双曲线的离心率为$\sqrt{2}$，则∠ABP的度数为（　　）
    A．30°B．60°C．120°D．30°或120°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（2$\sqrt{3}$，1），且以椭圆短轴的两个端点和一个焦点为顶点的三角形是等边三角形．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）设P（x，y）是椭圆E上的动点，M（2，0）为一定点，求|PM|的最小值及取得最小值时P点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．如图，菱形ABCD中，∠ABC=60°，AC与BD相交于点O，AE⊥平面ABCD，CF∥AE，AB=2，CF=3．
    （1）求证：BD⊥平面ACFE；
    （2）当直线FO与平面BED所成角的大小为45°时，求AE的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若sin（α-$\frac{π}{6}$）=$\frac{3}{5}$，α∈（0，$\frac{π}{2}$），则cosα的值为$\frac{4\sqrt{3}-3}{10}$．

    查看答案和解析>>

    同步练习册答案