
 如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.
如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.分析 (1)由AE⊥平面ABCD得出AE⊥BD,由菱形性质得BD⊥AC,故而BD⊥平面ACFE;
(2)以O为原点建立坐标系,设CF=a,求出$\overrightarrow{OF}$和平面BDE的法向量,利用直线FO与平面BED所成角的大小为45°,可得$\frac{a+3}{{\sqrt{10}\sqrt{{a^2}+1}}}=\frac{{\sqrt{2}}}{2}$,即可求出a的值.
解答 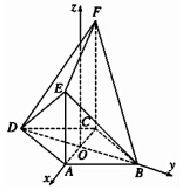 (1)证明:∵四边形ABCD是菱形,∴BD⊥AC.…(1分)
(1)证明:∵四边形ABCD是菱形,∴BD⊥AC.…(1分)
∵AE⊥平面ABCD,BD?平面ABCD,…(2分)
∴BD⊥AE,…(3分)
又AC?平面ACFE,AE?平面ACFE,AC∩AE=A,…(4分)
∴BD⊥平面ACFE.…(5分)
(2)解:以O为原点,以OA,OB所在直线分别为x轴,y轴,以过点O且平行于CF的直线为z轴建立空间直角坐标系.…(6分)
则$B({0,\sqrt{3},0}),D({0,-\sqrt{3},0}),F({-1,0,3})$.
设AE=a,则E(1,0,a),
∴$\overrightarrow{OF}=({-1,0,3}),\overrightarrow{DB}=({0,2\sqrt{3},0}),\overrightarrow{EB}=({-1,\sqrt{3},-a})$,…(7分)
设平面BDE的法向量为$\overrightarrow n=({x,y,z})$,则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{DB}=0\\ \overrightarrow n•\overrightarrow{EB}=0\end{array}\right.$…(8分)
即$\left\{\begin{array}{l}2\sqrt{3}y=0\\-x+\sqrt{3}y-az=0\end{array}\right.$令z=1,得$\overrightarrow n=({-a,0,1})$,…(9分)
∴$cos({\overrightarrow n,\overrightarrow{OF}})=\frac{{\overrightarrow n•\overrightarrow{OF}}}{{|{\overrightarrow n}||{\overrightarrow{OF}}|}}=\frac{a+3}{{\sqrt{10}\sqrt{{a^2}+1}}}$,…(10分)
∵直线FO与平面BED所成角的大小为45°,∴$\frac{a+3}{{\sqrt{10}\sqrt{{a^2}+1}}}=\frac{{\sqrt{2}}}{2}$,…(11分)
解得a=2或$a=-\frac{1}{2}$(舍),∴|AE|=2.…(12分)
点评 本题考查了线面垂直的判定,空间向量与空间角的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
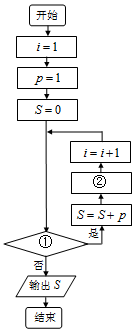 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$ | B. | {x|x<2} | C. | $\left\{{x\left|{x≤\frac{1}{2}或x>2}\right.}\right\}$ | D. | $\left\{{x\left|{\frac{1}{2}≤x<2}\right.}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com