
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
分析 根据对数函数的单调性,我们易判断出log220∈(4,5),结合已知中f(x+1)=f(x-1)且x∈(-1,0)时,f(x)=2x-1,利用函数的周期性与奇偶性,即可得到f(log220)的值.
解答 解:∵f(x+1)=f(x-1)
∴函数f(x)为周期为2的周期函数
又∵log232>log220>log216
∴4<log220<5
∴f(log220)=f(log220-4)=f(log2 $\frac{5}{4}$)=-f(-log2 $\frac{5}{4}$)
又∵x∈(-1,0)时,f(x)=2x-1
∴f(-log2 $\frac{5}{4}$)=-$\frac{1}{5}$,
故f(log220)=$\frac{1}{5}$.
故选:D.
点评 本题考查的知识点是函数的周期性和奇偶函数图象的对称性,其中根据已知中f(x+1)=f(x-1),求出函数的周期是解答的关键,属中档题.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:解答题
 如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.
如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
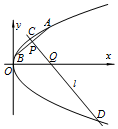 如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.
如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com