
分析 运用向量垂直的条件:数量积为0,以及数量积的性质:向量的平方即为模的平方,结合向量的夹角的余弦公式,计算即可得到所求值.
解答 解:非零向量$\overrightarrow{a}$,b满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥(3$\overrightarrow{a}$-$\overrightarrow{b}$),
可得($\overrightarrow{a}$+$\overrightarrow{b}$)•(3$\overrightarrow{a}$-$\overrightarrow{b}$)=0,
即有3$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$-$\overrightarrow{b}$2=0,
即为3+2$\overrightarrow{a}$•$\overrightarrow{b}$-4=0,
解得$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,
则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角余弦值为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{\frac{1}{2}}{1×2}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查向量数量积的夹角公式和性质,主要是向量的平方即为模的平方,向量垂直的条件:数量积为0,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
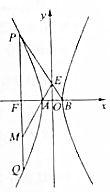 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{6}+1}}{4}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
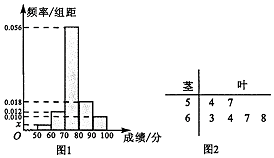 某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.
某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据的茎叶图如图2所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com