
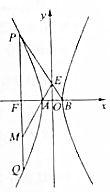
 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
分析 利用已知条件求出P的坐标,然后求解E的坐标,推出M的坐标,利用中点坐标公式得到双曲线的离心率即可.
解答 解:由题意可得P(-c,$\frac{{b}^{2}}{a}$), B(a,0),可得BP的方程为:y=-$\frac{{b}^{2}}{a(a+c)}$(x-a),
B(a,0),可得BP的方程为:y=-$\frac{{b}^{2}}{a(a+c)}$(x-a),
x=0时,y=$\frac{{b}^{2}}{a+c}$,E(0,$\frac{{b}^{2}}{a+c}$),A(-a,0),
则AE的方程为:y=$\frac{{b}^{2}}{a(a+c)}$(x+a),则M(-c,-$\frac{{b}^{2}(c-a)}{a(a+c)}$),
M是线段QF的中点,
可得:2$\frac{{b}^{2}(c-a)}{a(a+c)}$=$\frac{{b}^{2}}{a}$,
即2c-2a=a+c,
可得e=3.
故选:C.
点评 本题考查双曲线的简单性质的应用,考查转化思想以及计算能力.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
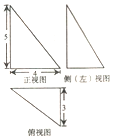 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )| A. | 200π | B. | 50π | C. | 100π | D. | $\frac{125\sqrt{2}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{64}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
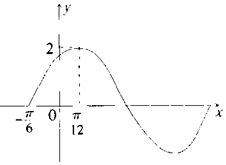 已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.
已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com