练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
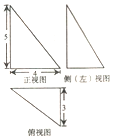
    9．《九章算术》是我国古代数学经典名著，它在集合学中的研究比西方早1千年，在《九章算术》中，将四个面均为直角三角形的四面体称为鳖臑，已知某“鳖臑”的三视图如图所示，则该鳖臑的外接球的表面积为（　　）
    A．200πB．50πC．100πD．$\frac{125\sqrt{2}}{3}$π

    分析 几何体复原为底面是直角三角形，一条侧棱垂直底面直角顶点的三棱锥，扩展为长方体，长方体的对角线的长，就是外接球的直径，然后求其的表面积．

    解答 解：由三视图复原几何体，几何体是底面是直角三角形，
    一条侧棱垂直底面直角顶点的三棱锥；扩展为长方体，也外接与球，
    它的对角线的长为球的直径：$\sqrt{9+16+25}$=5$\sqrt{2}$
    该三棱锥的外接球的表面积为：$4π•（\frac{5\sqrt{2}}{2}）^{2}$=50π，
    故选B．

    点评 本题考查三视图，几何体的外接球的表面积，考查空间想象能力，计算能力，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．在学期初，某班开展任课教师对特困生的帮扶活动，已知该班有3名青年任课教师与4名特困生结成帮扶关系，若这3名青年教师每位至少与一名学生结成帮扶关系，又这4名特困学生都能且只能得到一名教师的帮扶，那么不同的帮扶方案的种数为（　　）
    A．36B．72C．24D．48

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

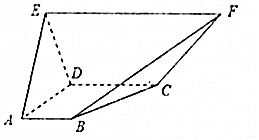    20．在如图所示的五面体中，面ABCD为直角梯形，∠BAD=∠ADC=$\frac{π}{2}$，平面ADE⊥平面ABCD，EF=2DC=4AB=4，△ADE是边长为2的正三角形．
    （Ⅰ）证明：BE⊥平面ACF；
    （Ⅱ）求二面角A-BC-F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位，则平移后的图象（　　）
    A．关于点$（-\frac{π}{12}，0）$对称B．关于直线$x=-\frac{π}{12}$对称
    C．关于点$（\frac{π}{12}，0）$对称D．关于直线$x=\frac{π}{12}$对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知等差数列{an}的前n项和为Sn，且满足S4=24，S7=63．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若bn=2an+an，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

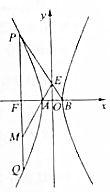    14．已知O为坐标原点，F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，A，B分别为左、右顶点，过点F做x轴的垂线交双曲线于点P，Q，连接PB交y轴于点E，连结AE交QF于点M，若M是线段QF的中点，则双曲线C的离心率为（　　）
    A．2B．$\frac{5}{2}$C．3D．$\frac{7}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．五个人负责一个社团的周一至周五的值班工作，每人一天，则甲同学不值周一，乙同学不值周五，且甲，乙不相邻的概率是（　　）
    A．$\frac{3}{10}$B．$\frac{7}{20}$C．$\frac{2}{5}$D．$\frac{13}{30}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知集合$M=\{x|\frac{2x-1}{x+1}≤1\}$，N={x|-1＜x＜1}，则（　　）
    A．M?NB．N?MC．M=ND．M∩N=∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设集合$A=[（x，y）|\frac{x^2}{25}+\frac{y^2}{16}≤1]，B=[（x，y）|\left\{\begin{array}{l}|x|≤m\\|y|≤n\end{array}\right.，0＜m＜5，0＜n＜4且（m，n）∈A]$，则集合∁AB对应图形面积取得最小值时，m+n的值为（　　）
    A．$\frac{{9\sqrt{2}}}{2}$B．$5\sqrt{2}$C．6D．8

    查看答案和解析>>

    同步练习册答案