
| A. | $\frac{3}{10}$ | B. | $\frac{7}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{13}{30}$ |
分析 基本事件总数n=${A}_{5}^{5}=120$,甲同学不值周一,乙同学不值周五,且甲,乙不相邻,甲乙排列有3种情况:①乙在周一,甲不在周五,乙x甲xx,乙不在周一,甲在周五,x乙xx甲,③乙不在周一,甲不在周五,x乙x甲x,由此求出甲同学不值周一,乙同学不值周五,且甲,乙不相邻包含贩基本事件个数,由此能求出结果.
解答 解:五个人负责一个社团的周一至周五的值班工作,每人一天,
基本事件总数n=${A}_{5}^{5}=120$,
甲同学不值周一,乙同学不值周五,
由题意得,甲不在周一,乙不在周五,且甲,乙不相邻,甲乙排列有3种情况:
①乙在周一,甲不在周五,乙x甲xx,排列数:${A}_{4}^{4}-{A}_{3}^{3}$=18,
②乙不在周一,甲在周五,x乙xx甲,排列数:${A}_{2}^{1}{A}_{3}^{3}$=12,
③乙不在周一,甲不在周五,x乙x甲x,排列数:${A}_{3}^{3}{A}_{2}^{2}$=12,
共有18+12+12=42,
∴甲同学不值周一,乙同学不值周五,且甲,乙不相邻的概率P=$\frac{42}{120}=\frac{7}{20}$.
故选:B.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:解答题
| ξ1 | 110 | 120 | 170 |
| P | m | 0.4 | n |
| X | 0 | 1 | 2 |
| ξ2 | 41.2 | 117.6 | 204.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
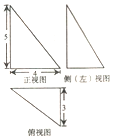 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )| A. | 200π | B. | 50π | C. | 100π | D. | $\frac{125\sqrt{2}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
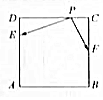 如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).
如图,正方形ABCD的边长为8,点E,F分别在边AD,BC上,且AE=3ED,CF=FB,如果对于常数m,在正方形ABC的四条边上有且只有6个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=m成立,那么m的取值范围是(-1,8).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
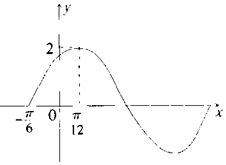 已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.
已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com