
| ξ1 | 110 | 120 | 170 |
| P | m | 0.4 | n |
| X | 0 | 1 | 2 |
| ξ2 | 41.2 | 117.6 | 204.0 |
分析 (Ⅰ)由离散型随机变量的分布列及数学期望的性质列出方程组,能求出m,n的值.
(Ⅱ)ξ2的可能取值为41.2,117.6,204,分虽求出相应的概率,由此能求出ξ2的分布列.
(Ⅲ)求出可得E(ξ2),由于该公司投资乙项目一年后能获得较多的利润,从而E(ξ2)>E(ξ1),由此能求出p的取值范围.
解答 解:(Ⅰ)由题意得$\left\{\begin{array}{l}m+0.4+n=1\\ 110m+120×0.4+170n=120\end{array}\right.$,
解得m=0.5,n=0.1.
(Ⅱ)ξ2的可能取值为41.2,117.6,204,
P(ξ2=41.2)=(1-p)[1-(1-p)]=p(1-p),
$P({ξ_2}=117.6)=p[{1-(1-p)}]+(1-p)(1-p)={p^2}+{(1-p)^2}$,
P(ξ2=204)=p(1-p),
所以ξ2的分布列为:
| ξ2 | 41.2 | 117.6 | 204 |
| P | p(1-p) | p2+(1-p)2 | p(1-p) |
点评 本题考查离散型随机变量的分布列及数学期望的求法及应用,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (0,$\frac{2}{3}$]∪[1,+∞) | C. | (0,$\frac{1}{2}$]∪[2,+∞) | D. | [$\frac{1}{2}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
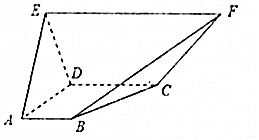 在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{7}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{13}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则a+c≤b+c | B. | 若a+c≤b+c,则a≤b | C. | 若a+c>b+c,则a>b | D. | 若a≤b,则a+c≤b+c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com