
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
分析 (1)根据题意可得频率,进而得到X,Y的分布列,利用相互独立事件的概率计算公式即可得出
P(X>100,Y>100).
(2)利用数学期望与方差的计算公式即可得出.
解答 解:(1)根据题意可得:X的分布列如下:
| X | 0 | 40 | 80 | 120 | 160 | 200 |
| P | $\frac{3}{30}$ | $\frac{5}{30}$ | $\frac{7}{30}$ | $\frac{7}{30}$ | $\frac{5}{30}$ | $\frac{3}{30}$ |
| Y | 0 | 40 | 80 | 120 | 160 | 200 |
| P | $\frac{4}{30}$ | $\frac{4}{30}$ | $\frac{6}{30}$ | $\frac{8}{30}$ | $\frac{5}{30}$ | $\frac{3}{30}$ |
点评 本题考查了相互独立事件的概率计算公式、随机变量的数学期望与方差的计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
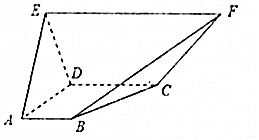 在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{7}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{13}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | N?M | C. | M=N | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则a+c≤b+c | B. | 若a+c≤b+c,则a≤b | C. | 若a+c>b+c,则a>b | D. | 若a≤b,则a+c≤b+c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $5\sqrt{2}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com