
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $5\sqrt{2}$ | C. | 6 | D. | 8 |
分析 由题意,求出椭圆的内接矩形面积最大值即可,利用基本不等式,结合面积公式可得结论.
解答 解:由题意,求出椭圆的内接矩形面积最大值即可,
由于$\frac{{m}^{2}}{25}+\frac{{n}^{2}}{16}$=1≥$\frac{mn}{10}$,∴mn≤10,∴S=4mn≤40,
当且仅当$\frac{{m}^{2}}{25}$=$\frac{{n}^{2}}{16}$=$\frac{1}{2}$,即m=$\frac{5\sqrt{2}}{2}$,n=2$\sqrt{2}$时,椭圆的内接矩形面积确定最大值,
∴m+n=$\frac{9\sqrt{2}}{2}$,
故选:A.
点评 本题考查椭圆方程的运用,考查基本不等式,考查学生分析解决问题的能力,属于中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
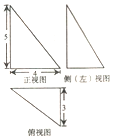 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )| A. | 200π | B. | 50π | C. | 100π | D. | $\frac{125\sqrt{2}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -$\frac{125}{8}$ | D. | $\frac{125}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
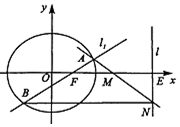 已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 原料 肥料 | A | B |
| 甲 | 3 | 1 |
| 乙 | 2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com