
| 原料 肥料 | A | B |
| 甲 | 3 | 1 |
| 乙 | 2 | 2 |
分析 (1)利用已知条件列出约束条件,然后画出可行域即可.
(2)写出目标函数,利用可行域,推出最优解,然后求解最大值.
解答 解:(1)由已知,x,y满足的关系式为:$\left\{\begin{array}{l}{3x+2y≤12}\\{x+2y≤8}\\{x≥0}\\{y≥0}\end{array}\right.$,不等式组表示的可行域为: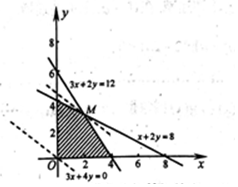 .
.
(2)设利润为z万元,则目标函数为:z=3x+4y,平移直线z=3x+4y,
可得目标函数经过M时,取得最大值,
由$\left\{\begin{array}{l}{3x+2y=12}\\{x+2y=8}\end{array}\right.$,可得M(2,3),
所以z的最大值为:3×2+4×3=18.
每日分别生产甲乙两种化肥各2,3吨,能够产生最大利润,最大利润为18万元.
点评 本题考查线性规划的简单应用,列出约束条件,判断最优解是解题的关键,考察转化思想以及计算能力.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | N?M | C. | M=N | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $5\sqrt{2}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{7}{12}$,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{4}$,$\frac{7}{12}$) | D. | ($\frac{1}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{8}-\frac{y^2}{24}=1$ | B. | $\frac{x^2}{24}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列{an}是单调递增数列,数列{bn}是单调递减数列 | |
| B. | 数列{an+bn}是等比数列 | |
| C. | 数列$\{\frac{a_n}{b_n}\}$有最小值,无最大值 | |
| D. | 若△ABC中,C=90°,CA=CB,则$|\overrightarrow{{B_n}{A_n}}|$最小时,${a_n}+{b_n}=\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.
自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元.| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
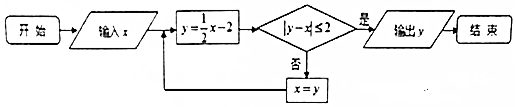
| A. | 2 | B. | -1 | C. | -$\frac{13}{4}$ | D. | -$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
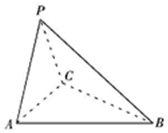 如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.
如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com