练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．设i是虚数单位，复数$\frac{a+i}{1+i}$为纯虚数，则实数a的值为（　　）
    A．-1B．1C．-2D．2

    分析 由复数代数形式的乘除运算化简$\frac{a+i}{1+i}$，由整理出实部和虚部，由纯虚数的定义列出方程组，求出a的值．

    解答 解：由题意得，$\frac{a+i}{1+i}$=$\frac{（a+i）（1-i）}{（1+i）（1-i）}$=$\frac{a+1+（1-a）i}{2}$
    =$\frac{a+1}{2}+\frac{a-1}{2}i$，
    因为复数$\frac{a+i}{1+i}$为纯虚数，所以$\left\{\begin{array}{l}{\frac{a+1}{2}=0}\\{\frac{a-1}{2}≠0}\end{array}\right.$，
    解得a=-1，
    故选A．

    点评 本题考查复数代数形式的乘除运算，以及纯复数的定义的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知x，y∈R，i是虚数单位．若x+yi与$\frac{3+i}{1+i}$互为共轭复数，则x+y=（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在学期初，某班开展任课教师对特困生的帮扶活动，已知该班有3名青年任课教师与4名特困生结成帮扶关系，若这3名青年教师每位至少与一名学生结成帮扶关系，又这4名特困学生都能且只能得到一名教师的帮扶，那么不同的帮扶方案的种数为（　　）
    A．36B．72C．24D．48

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知实数x，y满足$\left\{{\begin{array}{l}{x+y-4≤0}\\{2x-y+1≥0}\\{x-2y+2≥0}\end{array}}\right.$，则x+3y的最大值为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设$\frac{i}{1+i}$=a+bi（a，b∈R，i为虚数单位），则|a-bi|=（　　）
    A．1B．$\frac{1}{2}$C．$\sqrt{2}$D．$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．定义在R上的奇函数f（x）满足：f（x+1）=f（x-1），且当-1＜x＜0时，f（x）=2x-1，则f（log220）等于（　　）
    A．$\frac{1}{4}$B．-$\frac{1}{4}$C．-$\frac{1}{5}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

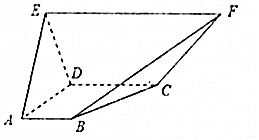    20．在如图所示的五面体中，面ABCD为直角梯形，∠BAD=∠ADC=$\frac{π}{2}$，平面ADE⊥平面ABCD，EF=2DC=4AB=4，△ADE是边长为2的正三角形．
    （Ⅰ）证明：BE⊥平面ACF；
    （Ⅱ）求二面角A-BC-F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位，则平移后的图象（　　）
    A．关于点$（-\frac{π}{12}，0）$对称B．关于直线$x=-\frac{π}{12}$对称
    C．关于点$（\frac{π}{12}，0）$对称D．关于直线$x=\frac{π}{12}$对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知集合$M=\{x|\frac{2x-1}{x+1}≤1\}$，N={x|-1＜x＜1}，则（　　）
    A．M?NB．N?MC．M=ND．M∩N=∅

    查看答案和解析>>

    同步练习册答案