
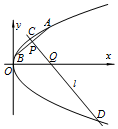
 如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.
如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.分析 (Ⅰ)设AB直线方程,与抛物线C:y2=4x联立,利用韦达定理,求出直线l的方程,即可求点Q的坐标;
(Ⅱ)(方法一)A,B,C,D四点共圆,有$\frac{1}{4}|CD{|^2}=\frac{1}{4}|AB{|^2}+|PM{|^2}$,即可求直线l的方程.
(方法二)利用参数方程求.
解答 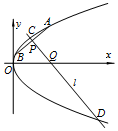 解:(Ⅰ)易知AB不与x轴垂直,设AB直线方程为:y=k(x-2)+t,
解:(Ⅰ)易知AB不与x轴垂直,设AB直线方程为:y=k(x-2)+t,
与抛物线C:y2=4x联立,消去y得:k2x2+(2tk-4k2-4)x+(t-2k)2=0,
∴△=(4k2+4-2tk)2-4k2×(t-2k)2>0(i)
设A(x1,y1),B(x2,y2),则x1,x2是上述方程两根,
∴x1+x2=$\frac{{4{k^2}+4-2tk}}{k^2}=4$,
即tk=2,代入(i)中,求得$-2\sqrt{2}<t<2\sqrt{2}$且t≠0,
∴直线l的方程为:y-t=$-\frac{t}{2}$(x-2),
令y=0,得x=4,知定点坐标为(4,0);…(5分)
(Ⅱ)(方法一)|AB|=$\sqrt{1+{k^2}}|{x_1}-{x_2}|=\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$
=$\sqrt{1+{k^2}}\sqrt{{4^2}-4×\frac{{{{(t-2k)}^2}}}{k^2}}$=$\sqrt{1+{k^2}}•\sqrt{{4^2}-4×\frac{{{{(t-2k)}^2}}}{k^2}}=\sqrt{{t^2}+4}•\sqrt{8-{t^2}}$,…(7分)
CD直线:$y=-\frac{t}{2}(x-4)$,与抛物线y2=4x联立,消去y得:t2x2-(8t2+16)x+16t2=0,
设C(x3,y3),D(x4,y4),
∴x3+x4=$\frac{{8{t^2}+16}}{t^2}=8+\frac{16}{t^2}$,x3x4=16,…(8分)
设CD的中点为M(x0,y0),
∴x0=$4+\frac{8}{t^2}$,y0=$-\frac{4}{t}$,|PM|=$\frac{{{t^2}+4}}{t^2}×\sqrt{4+{t^2}}$,
∴|CD|=$\sqrt{1+{{\frac{t}{4}}^2}}|{x_3}-{x_4}|$=$\sqrt{1+{{\frac{t}{4}}^2}}\sqrt{{{({x_3}+{x_4})}^2}-4{x_3}{x_4}}$=$\sqrt{1+{{\frac{t}{4}}^2}}\sqrt{{{(8+\frac{16}{t^2})}^2}-4×16}$
=$\sqrt{4+{t^2}}\sqrt{{{(4+\frac{8}{t^2})}^2}-16}=8×\sqrt{4+{t^2}}×\sqrt{\frac{1}{t^4}+\frac{1}{t^2}}$,
∴A,B,C,D四点共圆,有$\frac{1}{4}|CD{|^2}=\frac{1}{4}|AB{|^2}+|PM{|^2}$,
代入并整理得t4-12t2+32=0,求得t2=4或t2=8(舍去),t=±2.
∴直线l的方程为y=x-4或y=-x+4.…(12分)
(方法二)利用参数方程求:
设AB直线的参数方程为:$\left\{\begin{array}{l}x=2+mcosθ\\ y=t+msinθ\end{array}\right.$,
代入抛物线C:y2=4x得,sin2θm2+2sinθmt-4cosθm+t2-8=0,${m_1}{m_2}=\frac{{{t^2}-8}}{{{{sin}^2}θ}}$,$|PA|•|PB|=-{m_1}{m_2}=\frac{{8-{t^2}}}{{{{sin}^2}θ}}$,
则直线CD的参数方程为:$\left\{\begin{array}{l}x=2+mcosβ\\ y=t+msinβ\end{array}\right.$,$β=θ+\frac{π}{2}$或$β=θ-\frac{π}{2}$
有${m_3}{m_4}=\frac{{{t^2}-8}}{{{{sin}^2}β}}$,$|PC|•|PD|=-{m_3}{m_4}=\frac{{8-{t^2}}}{{{{sin}^2}β}}$,sin2β=cos2θ,
依题意有:|PA|•|PB|=|PC|•|PD|,sin2θ=cos2θ,则有$θ=\frac{π}{4}$或$\frac{3π}{4}$,
∴直线l的方程为y=x-4或y=-x+4.…(12分)
点评 本题考查直线过定点,考查直线方程,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1,3,4} | B. | {-1,1,3} | C. | {1,3} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{6}+1}}{4}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com