
分析 (1)当n=1求得a1,当n≥2,由an=Sn-Sn-1,代入验证当n=1是否成立,即可求得数列{an}的通项公式;
(2)由(1)求得数列{bn}通项公式,根据新定义即可求得
解答 解:(1)当n=1时,a1=S1=ln2-a;当n≥2且n∈N*时,${a_n}={S_n}-{S_{n-1}}=ln({n+1})-a-({lnn-a})=ln({n+1})-a-lnn+a=ln({n+1})-lnn=ln\frac{n+1}{n}$,
当a=0时,a1=ln2,适合此等式,当a≠0时,a1=ln2-a≠ln2,不适合此等式,
∴当a=0时,${a_n}=ln\frac{n+1}{n}({n∈{N^*}})$;
当a≠0时,${a_n}=\left\{{\begin{array}{l}{ln2-a,n=1}\\{ln\frac{n+1}{n},n≥2}\end{array}}\right.$.
(2)当a=0时,${b_n}={e^{a_n}}={e^{ln\frac{n+1}{n}}}=\frac{n+1}{n}$,
∴$\sum_{k=1}^n{{b_k}={b_1}•{b_2}•{b_3}•…•{b_n}=\frac{2}{1}×\frac{3}{2}×\frac{4}{3}×…×\frac{n+1}{n}}=n+1$.
当a≠0时,${b_n}={e^{a_n}}=\left\{{\begin{array}{l}{\frac{2}{e^a},n=1}\\{ln\frac{n+1}{n},n≥2}\end{array}}\right.$,
∴$\sum_{k=1}^n{{b_k}={b_1}•{b_2}•{b_3}•…•{b_n}={e^{\frac{2}{a}}}×\frac{3}{2}×\frac{4}{3}×…×\frac{n+1}{n}={e^{\frac{n+1}{a}}}}$.
综上,$\sum_{k=1}^n{{b_k}=\frac{n+1}{e^a}}$.
点评 本题考查求数列的通项公式的方法,考查数列应用,考查分析问题及解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
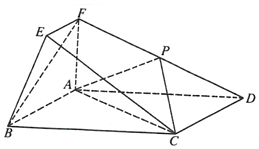 在如图所示的几何体中,四边形ABCD为矩形,直线AF⊥平面ABCD,EF∥AB,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,直线AF⊥平面ABCD,EF∥AB,AD=2,AB=AF=2EF=1,点P在棱DF上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 30°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.
如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
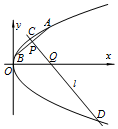 如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.
如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com