
分析 根据题意,可以将ab转化可得ab=$\frac{1}{2+\frac{b}{a}}$+$\frac{2}{2+\frac{a}{b}}$,令$\frac{b}{a}$=t,则ab又可以变形为ab=1+$\frac{t-1}{2{t}^{2}+5t+2}$,再令u=t-1,ab进一步可以变形为ab=1+$\frac{1}{2u+\frac{9}{u}+9}$,利用基本不等式,计算可得答案.
解答 解:根据题意,由于$\frac{1}{{({2a+b})b}}+\frac{2}{{({2b+a})a}}=1$,
则ab=ab($\frac{1}{{({2a+b})b}}+\frac{2}{{({2b+a})a}}$)=$\frac{a}{2a+b}$+$\frac{2b}{2b+a}$=$\frac{1}{2+\frac{b}{a}}$+$\frac{2}{2+\frac{a}{b}}$;
令$\frac{b}{a}$=t,
则ab=$\frac{1}{2+t}$+$\frac{2}{2+\frac{1}{t}}$=$\frac{1}{2+t}$+$\frac{2t}{2t+1}$=$\frac{2t+1+2t(2+t)}{(2+t)(2t+1)}$=$\frac{2{t}^{2}+6t+1}{2{t}^{2}+5t+2}$=1+$\frac{t-1}{2{t}^{2}+5t+2}$,
令u=t-1,t=u+1;
ab=1+$\frac{u}{2(u+1)^{2}+5(u+1)+2}$=1+$\frac{u}{2{u}^{2}+9u+9}$=1+$\frac{1}{2u+\frac{9}{u}+9}$≤1+$\frac{1}{2\sqrt{18}+9}$=2-$\frac{2\sqrt{2}}{3}$;
即ab的最大值2-$\frac{2\sqrt{2}}{3}$;
故答案为:2-$\frac{2\sqrt{2}}{3}$.
点评 本题考查基本不等式的应用,关键是利用$\frac{1}{{({2a+b})b}}+\frac{2}{{({2b+a})a}}=1$,借助恒等变形将问题进行转化.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
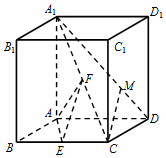 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
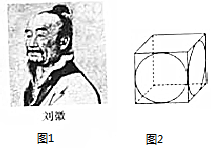 我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )| A. |  | B. | 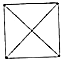 | C. | 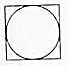 | D. | 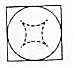 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{27}=1$ | B. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{10}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 80 | C. | 15 | D. | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
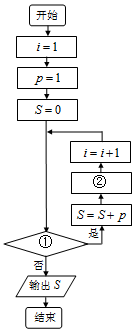 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com