
分析 (1)根据题意,若m=0时,原不等式为:x|x|-2≥0,进而变形可得$\left\{\begin{array}{l}{x≥0}\\{{x}^{2}≥2}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{-{x}^{2}≥2}\end{array}\right.$,解可得x的取值范围,即可得答案;
(2)根据题意,由x∈[2,3],将原不等式变形可得:|x-m|≥$\frac{m+2}{x}$,①,分m≤-2与m>-2两种情况讨论,分别求出m的取值范围,综合可得答案.
解答 解:(1)根据题意,当m=0时,原不等式为:x|x|-2≥0,
等价于$\left\{\begin{array}{l}{x≥0}\\{{x}^{2}≥2}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{-{x}^{2}≥2}\end{array}\right.$,
解可得x≥$\sqrt{2}$,
故原不等式的解集为{x|x≥$\sqrt{2}$};
(2)当x∈[2,3]时,原不等式变形可得:|x-m|≥$\frac{m+2}{x}$,①
当m≤-2时,m+2≤0,①式恒成立;
当m>-2时,即m+2>0时,
①式等价于x-m≥$\frac{m+2}{x}$或x-m≤-$\frac{m+2}{x}$,
化简可得:x2-2≥m(x+1)或x2+2≤m(x+1),②
又由x∈[2,3],则有x+1>0且x-1>0,
则②可以变形为m≤$\frac{{x}^{2}-2}{x+1}$或m≥$\frac{{x}^{2}+2}{x-1}$;
又由$\frac{{x}^{2}-2}{x+1}$=x-$\frac{1}{x+1}$-1,$\frac{{x}^{2}+2}{x-1}$=x-1+$\frac{3}{x-1}$+2;
又由x∈[2,3],则($\frac{{x}^{2}-2}{x+1}$)min=$\frac{2}{3}$,($\frac{{x}^{2}+2}{x-1}$)max=6;
则有m≤$\frac{2}{3}$或m≥6;
故m的取值范围是{m|m≤$\frac{2}{3}$或m≥6}.
点评 本题考查绝对值不等式的运用以及解法,关键是熟练掌握绝对值三角不等式.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$ | B. | {x|x<2} | C. | $\left\{{x\left|{x≤\frac{1}{2}或x>2}\right.}\right\}$ | D. | $\left\{{x\left|{\frac{1}{2}≤x<2}\right.}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
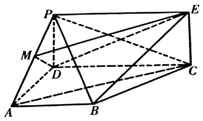 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1,3,4} | B. | {-1,1,3} | C. | {1,3} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com