
 .
. 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围; 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.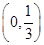 (2)
(2)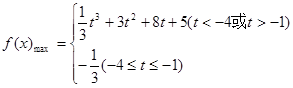
 求导,获得导函数
求导,获得导函数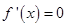 的根与大于0小于0的解集,获得函数
的根与大于0小于0的解集,获得函数 的单调区间和极值点,极值.进而确定函数
的单调区间和极值点,极值.进而确定函数 在区间
在区间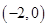 上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在
上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在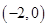 上要有两个零点,需要
上要有两个零点,需要 满足
满足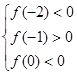 即可,解不等式即可求出
即可,解不等式即可求出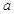 的取值范围.
的取值范围.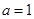 ,则利用(1)可以得到
,则利用(1)可以得到 的单调性以及极值点,极值.要得到函数
的单调性以及极值点,极值.要得到函数 在含参数的区间
在含参数的区间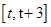 上的最大值,我们需要讨论
上的最大值,我们需要讨论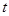 的范围得到函数
的范围得到函数 的在区间
的在区间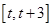 上的单调性进而得到
上的单调性进而得到 在该区间上的最大值,为此分三种情况分别为
在该区间上的最大值,为此分三种情况分别为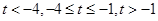 ,依次确定单调性得到最大值即可.
,依次确定单调性得到最大值即可.
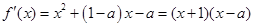 , (1分)
, (1分)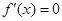 ,解得
,解得 (2分)
(2分)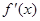 ,
, 的变化情况如下表:
的变化情况如下表: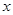 | 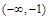 | 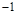 | 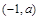 | 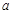 | 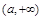 |
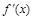 | 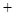 | 0 | — | 0 | 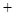 |
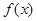 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 的单调递增区间为(-∞,-1),(a,+∞);单调递减区间为(-1,a);(4分)
的单调递增区间为(-∞,-1),(a,+∞);单调递减区间为(-1,a);(4分) 在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,要使函数
在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,要使函数 在区间
在区间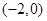 内恰有两个零点,当且仅当
内恰有两个零点,当且仅当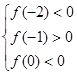 , (5分)
, (5分)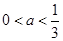 , 所以a的取值范围是(0,
, 所以a的取值范围是(0,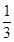 ). (6分)
). (6分)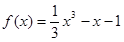 . 由(1)可知,函数
. 由(1)可知,函数 的单调递增区间为(-∞,-1),(1,+∞);单调递减区间为(-1,1);
的单调递增区间为(-∞,-1),(1,+∞);单调递减区间为(-1,1);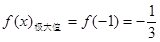 . (7分)
. (7分) 在区间[t,t+3]上单调递增,所以
在区间[t,t+3]上单调递增,所以 在区间[t,t+3]上的最大值为
在区间[t,t+3]上的最大值为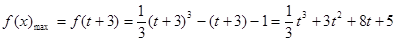 ; (9分)
; (9分)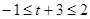 ,即
,即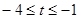 时,
时, 在区间
在区间 上单调递增,在区间[-1,1]上单调递减,在区间[1,2]上单调递增,且
上单调递增,在区间[-1,1]上单调递减,在区间[1,2]上单调递增,且 ,所以
,所以 在区间
在区间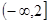 上的最大值为
上的最大值为 . (10分)
. (10分)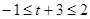 ,即
,即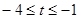 时,有[t,t+3]Ì
时,有[t,t+3]Ì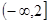 ,-1Î[t,t+3],所以
,-1Î[t,t+3],所以 在
在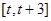 上的最大值为
上的最大值为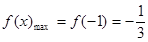 ; (11分)
; (11分) 在区间
在区间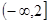 上的最大值为
上的最大值为 .
.  在区间(1,+∞)上单调递增,所以
在区间(1,+∞)上单调递增,所以 ,
, 在
在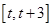 上的最大值为
上的最大值为 . (13分)
. (13分) 在[t,t+3]上的最大值
在[t,t+3]上的最大值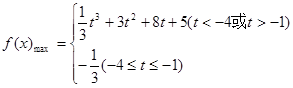 . (14分)
. (14分)

科目:高中数学 来源:不详 题型:解答题
 .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 在区间
在区间 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 x3+
x3+ x2+2ax.
x2+2ax. ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围. ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com