
【题目】已知四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() 且
且![]() ,E为PA的中点.
,E为PA的中点.
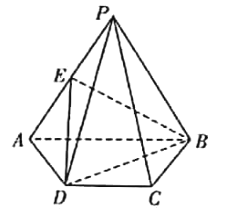
(Ⅰ)求证:![]() 平面PBC;
平面PBC;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,推导出四边形
,推导出四边形![]() 为平行四边形,从而
为平行四边形,从而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,以
,以![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
证明:(Ⅰ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
由已知得![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
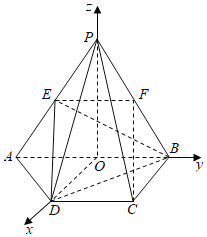
(Ⅱ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,又平面
,又平面![]() 平面ABCD,所以
平面ABCD,所以![]() 平面ABCD,
平面ABCD,
所以![]() ,由已知得
,由已知得![]() ,
,
以OD,OB,OP分别为x,y,z轴,建立空间直角坐标系![]() ,
,
设![]() ,故
,故![]() ,
,
所以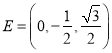 .
.
设平面EBD的法向量为![]() ,则
,则![]() ,
,
又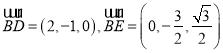 ,
,
所以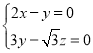 ,取
,取![]() ,即
,即![]() .
.
又平面BDC的法向量为![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
所以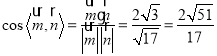 .
.
又二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】把编号为1,2,3,4,5的五个大小、形状相同的小球,随机放入编号为1,2,3,4,5的五个盒子里.每个盒子里放入一个小球.
(1)求恰有两个球的编号与盒子的编号相同的概率;
(2)设恰有![]() 个小球的编号与盒子编号相同,求随机变量
个小球的编号与盒子编号相同,求随机变量![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,以
的中点,以![]() 为圆心,
为圆心, ![]() 为半径的圆交
为半径的圆交![]() 于
于![]() ,点
,点![]() 在弧
在弧![]() 上运动(如图).若
上运动(如图).若![]() ,其中
,其中![]() ,
, ![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将4名大学生随机安排到A,B,C,D四个公司实习.
(1)求4名大学生恰好在四个不同公司的概率;
(2)随机变量X表示分到B公司的学生的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖南省会城市长沙又称星城,是楚文明和湖湘文化的发源地,是国家首批历史文化名城.城内既有岳麓山、橘子洲等人文景观,又有岳麓书院、马王堆汉墓等名胜古迹,每年都有大量游客来长沙参观旅游.为合理配置旅游资源,管理部门对首次来岳麓山景区游览的游客进行了问卷调查,据统计,其中![]() 的人计划只游览岳麓山,另外
的人计划只游览岳麓山,另外![]() 的人计划既游览岳麓山又参观马王堆.每位游客若只游览岳麓山,则记1分;若既游览岳麓山又参观马王堆,则记2分.假设每位首次来岳麓山景区游览的游客计划是否参观马王堆相互独立,视频率为概率.
的人计划既游览岳麓山又参观马王堆.每位游客若只游览岳麓山,则记1分;若既游览岳麓山又参观马王堆,则记2分.假设每位首次来岳麓山景区游览的游客计划是否参观马王堆相互独立,视频率为概率.
(1)从游客中随机抽取3人,记这3人的合计得分为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)从游客中随机抽取![]() 人(
人(![]() ),记这
),记这![]() 人的合计得分恰为
人的合计得分恰为![]() 分的概率为
分的概率为![]() ,求
,求![]() ;
;
(3)从游客中随机抽取若干人,记这些人的合计得分恰为![]() 分的概率为
分的概率为![]() ,随着抽取人数的无限增加,
,随着抽取人数的无限增加,![]() 是否趋近于某个常数?若是,求出这个常数;若不是,说明理由.
是否趋近于某个常数?若是,求出这个常数;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
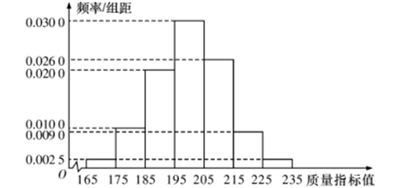
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,满足
上一点,满足![]() ,
,![]() 为
为![]() 的中点,现将梯形沿
的中点,现将梯形沿![]() 折叠(如图2),使平面
折叠(如图2),使平面![]() 平面
平面![]() .
.
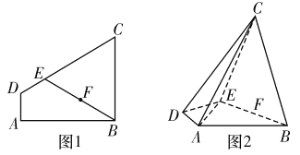
(1)求证:平面![]() 平面
平面![]() ;
;
(2)能否在线段![]() 上找到一点
上找到一点![]() (端点除外)使得直线
(端点除外)使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com