
 已知异面直线a,b,A∈a,B∈b,AB的中点为O,平面α满足a∥α,
已知异面直线a,b,A∈a,B∈b,AB的中点为O,平面α满足a∥α,分析 (1)连接AN交平面α 于Q,连接OQ、PQ,推导出BN∥OQ,PQ∥AM,由此能证明P为MN的中点.
(2)推导出OQ=3,PQ=4,∠PQO=60°,或∠PQO=120°,由此能求出OP的长.
解答 证明:(1)连接AN交平面 α 于Q,连接OQ、PQ,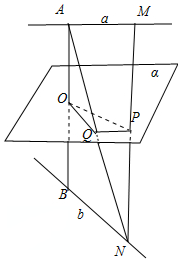
∵A∉b,∴A、b可确定平面β,
∴α∩β=OQ,由b∥α 得 BN∥OQ.
∵O为AB的中点,∴Q为AN的中点.
同理 PQ∥AM,故P为MN的中点.
解:(2)由(1)得OQ∥BN,且OQ=$\frac{1}{2}$BN=3,
PQ∥AM,且PQ=$\frac{1}{2}$AM=4,
∵a,b所成的角为600,∴∠PQO=60°或∠PQO=120°,
当∠PQO=60°时,
OP=$\sqrt{O{Q}^{2}+P{Q}^{2}-2×OQ×PQ×cos∠PQO}$
=$\sqrt{9+16-2×3×4×\frac{1}{2}}$=$\sqrt{13}$;
当∠PQO=120°时,
OP=$\sqrt{O{Q}^{2}+P{Q}^{2}-2×OQ×PQ×cos∠PQO}$
=$\sqrt{9+16+2×3×4×\frac{1}{2}}$=$\sqrt{37}$.
∴OP的长为$\sqrt{13}$或$\sqrt{37}$.
点评 本题考查点为线段中点的证明,考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
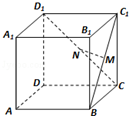 如图,在正方体ABCD-A1B1C1D1中,M、N分别是BC1、CD1的中点,则下列说法错误的是( )
如图,在正方体ABCD-A1B1C1D1中,M、N分别是BC1、CD1的中点,则下列说法错误的是( )| A. | MN∥AB | B. | MN⊥AC | C. | MN⊥CC1 | D. | MN∥平面ABCD |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-∞,0] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图(两图都不完整),则下列结论中错误的是( )
如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图(两图都不完整),则下列结论中错误的是( )| A. | 该班总人数为50人 | B. | 步行人数为30人 | ||
| C. | 骑车人数占总人数的20% | D. | 乘车人数是骑车人数的2.5倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
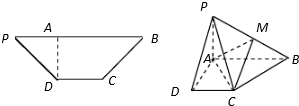 已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=$\sqrt{2}$,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.
已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=$\sqrt{2}$,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com