
分析 (1)根据换元法求出f(x)的解析式即可;(2)求出g(x)的解析式,得到g(x)的导数,根据函数的单调性求出a的范围即可.
解答 解:(1)∵f(1+$\frac{1}{x}$)=$\frac{1}{x^2}$-1,
令1+$\frac{1}{x}$=t,则$\frac{1}{x}$=t-1,
则f(t)=(t-1)2-1=t2-2t(t≠0),
故f(x)=x2-2x,(x≠0);
(2)g(x)=$\frac{{a{x^2}+x}}{f(x)}$=$\frac{ax+1}{x-2}$,(x>2),
g′(x)=$\frac{-2a-1}{{(x-2)}^{2}}$,
若g(x)在(2,+∞)递增,
则$\frac{-2a-1}{{(x-2)}^{2}}$>0在(2,+∞)恒成立,
故-2a-1>0,即a<-$\frac{1}{2}$.
点评 本题考查了求函数的解析式问题,考查函数的单调性问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±(2+$\sqrt{3}$) | D. | $±\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知异面直线a,b,A∈a,B∈b,AB的中点为O,平面α满足a∥α,
已知异面直线a,b,A∈a,B∈b,AB的中点为O,平面α满足a∥α,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
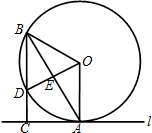 如图AB是⊙O的一条弦,过点A作圆的切线l,过点B作BC⊥l,垂足是C,BC与⊙O交于点D,已知$AC=2\sqrt{3}$,CD=2.
如图AB是⊙O的一条弦,过点A作圆的切线l,过点B作BC⊥l,垂足是C,BC与⊙O交于点D,已知$AC=2\sqrt{3}$,CD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com