
 )都在函数f(x)=x+
)都在函数f(x)=x+ 的图象上.
的图象上. }的前n项积,是否存在实数a,使得不等式An
}的前n项积,是否存在实数a,使得不等式An 对一切n∈N*都成立?若存在,求出a的取值范围,若不存在,说明理由.
对一切n∈N*都成立?若存在,求出a的取值范围,若不存在,说明理由.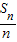 =n+
=n+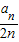 ,Sn=n2+
,Sn=n2+ an,令n=1,2,3,分别求出a1,a2,a3,然后仔细观察,总结规律,猜想:an=2n(n∈N*),再用用数字归纳法证明.
an,令n=1,2,3,分别求出a1,a2,a3,然后仔细观察,总结规律,猜想:an=2n(n∈N*),再用用数字归纳法证明.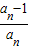 =1-
=1-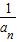 ,知An=(1-
,知An=(1- )(1-
)(1-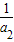 )(1-
)(1-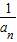 ),An
),An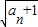 =(1-
=(1-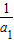 )(1-
)(1-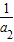 )(1-
)(1-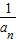 )
)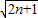 ,又f(a)-
,又f(a)- =a+
=a+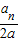 -
-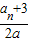 =a-
=a-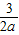 ,故An
,故An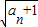 <f(a)-
<f(a)-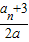 对一切n∈N*都成立,由此能够推导出使得所给不等式对一切n∈N*都成立的实数a存在,并且能求出a的取值范围.
对一切n∈N*都成立,由此能够推导出使得所给不等式对一切n∈N*都成立的实数a存在,并且能求出a的取值范围.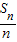 )都在函数f(x)=x+
)都在函数f(x)=x+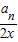 的图象上,故
的图象上,故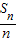 =n+
=n+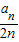 .
. an,令n=1得a1=1+
an,令n=1得a1=1+ a1,∴a1=2
a1,∴a1=2 a2,∴a2=4
a2,∴a2=4 a3,∴a3=6
a3,∴a3=6 ak,Sk+1=(k+1)2+
ak,Sk+1=(k+1)2+ ak+1,
ak+1, ak+1-
ak+1- ak,
ak,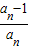 =1-
=1-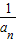 ,故An=(1-
,故An=(1-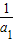 )(1-
)(1-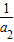 )(1-
)(1-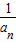 ),
),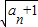 =(1-
=(1-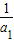 )(1-
)(1-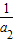 )(1-
)(1-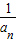 )
)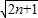
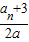 =a+
=a+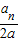 -
-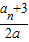 =a-
=a-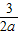
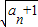 <f(a)-
<f(a)-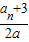 对一切n∈N*都成立,就是
对一切n∈N*都成立,就是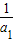 )(1-
)(1-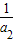 )(1-
)(1-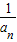 )•
)•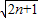 <a-
<a-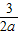 对一切n∈N*都成立.(8分)
对一切n∈N*都成立.(8分)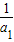 )(1-
)(1-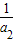 )(1-
)(1-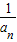 )
)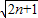 ,则只需g(n)max<a-
,则只需g(n)max<a-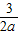 即可.(9分)
即可.(9分)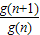 =(1-
=(1-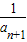 )•
)•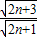 =
=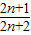 •
•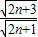
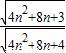 <1
<1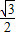 ,(12分)
,(12分)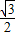 <a-
<a-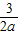 得
得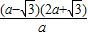 >0解得-
>0解得-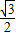 <a<0或a>
<a<0或a>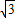 .
.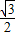 ,0)∪(
,0)∪(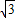 ,+∞).(14分)
,+∞).(14分)

科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 10 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| Sn |
| 5•2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com