Question

已知函数f（x）=xe^-x（x∈R）
（Ⅰ）求函数f（x）的单调区间和极值；
（Ⅱ）已知函数y=g（x）的图象与函数y=f（x）的图象关于直线x=1对称，证明：当x＞1时，f（x）＞g（x）；
（Ⅲ）如果x₁≠x₂，且f（x₁）=f（x₂），证明x₁+x₂＞2．

Answer 1

分析：（1）先求导求出导数为零的值，通过列表判定导数符号，确定出单调性和极值．
（2）先利用对称性求出g（x）的解析式，比较两个函数的大小可将它们作差，研究新函数的最小值，使最小值大于零，不等式即可证得．
（3）通过题意分析先讨论，可设x₁＜1，x₂＞1，利用第二问的结论可得f（x₂）＞g（x₂），根据对称性将g（x₂）换成f（2-x₂），再利用单调性根据函数值的大小得到自变量的大小关系．

解答：解：（Ⅰ）解：f′（x）=（1-x）e^-x
令f′（x）=0，解得x=1
当x变化时，f′（x），f（x）的变化情况如下表

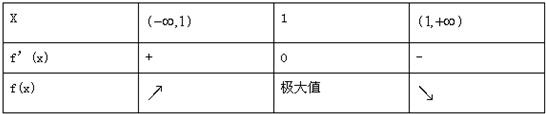
所以f（x）在（-∞，1）内是增函数，在（1，+∞）内是减函数．
函数f（x）在x=1处取得极大值f（1）且f（1）=

1

e

．

（Ⅱ）证明：由题意可知g（x）=f（2-x），得g（x）=（2-x）e^x-2
令F（x）=f（x）-g（x），即F（x）=xe^-x+（x-2）e^x-2
于是F'（x）=（x-1）（e^2x-2-1）e^-x
当x＞1时，2x-2＞0，从而e^2x-2-1＞0，又e^-x＞0，所以f′（x）＞0，从而函数F（x）在[1，+∞）是增函数．
又F（1）=e^-1-e^-1=0，所以x＞1时，有f（x）＞F（1）=0，即f（x）＞g（x）．

（Ⅲ）证明：（1）若（x₁-1）（x₂-1）=0，由（I）及f（x₁）=f（x₂），则x₁=x₂=1．与x₁≠x₂矛盾．
（2）若（x₁-1）（x₂-1）＞0，由（I）及f（x₁）=f（x₂），得x₁=x₂．与x₁≠x₂矛盾．
根据（1）（2）得（x₁-1）（x₂-1）＜0，不妨设x₁＜1，x₂＞1．
由（Ⅱ）可知，f（x₂）＞g（x₂），
则g（x₂）=f（2-x₂），
所以f（x₂）＞f（2-x₂），
从而f（x₁）＞f（2-x₂）．
因为x₂＞1，所以2-x₂＜1，
又由（Ⅰ）可知函数f（x）在区间（-∞，1）内是增函数，
所以x₁＞2-x₂，即x₁+x₂＞2．

点评：本小题主要考查导数的应用，利用导数研究函数的单调性与极值等基础知识，考查运算能力及用函数思想分析解决问题的能力．