
【题目】函数![]() (a为常数,且
(a为常数,且![]() )在
)在![]() 处取得极值.
处取得极值.
(1)求实数a的值,并求![]() 的单调区间;
的单调区间;
(2)关于x的方程![]() 在
在![]() 上恰有1个实数根,求实数b的取值范围;
上恰有1个实数根,求实数b的取值范围;
(3)求证:当![]() 时,
时,![]() .
.
【答案】(1)![]() ,
,![]() 的单调递增区间是
的单调递增区间是![]() ,函数
,函数![]() 的单调递减区间是
的单调递减区间是![]() .(2)
.(2)![]() .(3)见解析
.(3)见解析
【解析】
(1)首先写出函数的定义域,之后求函数的导函数,利用条件,得到等式![]() ,解出
,解出![]() ,代入导函数解析式,令
,代入导函数解析式,令![]() ,
,![]() ,求得函数的单调增、减区间;
,求得函数的单调增、减区间;
(2)将![]() 的解析式代入方程,化简得
的解析式代入方程,化简得![]() ,令
,令![]() ,利用导数研究其单调性,结合题意,得到不等式组,求得结果;
,利用导数研究其单调性,结合题意,得到不等式组,求得结果;
(3)结合(1),得到![]() ,进一步得到
,进一步得到![]() 成立,对
成立,对![]() 依次取值,累加得到结果.
依次取值,累加得到结果.
(1)![]() ,
,![]() ,由题意得,
,由题意得,![]() ,
,
得![]() ,
,
当![]() 时,
时,![]() ,
,
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
∴函数![]() 的单调递增区间是
的单调递增区间是![]() ,
,
函数![]() 的单调递减区间是
的单调递减区间是![]() .
.
(2)关于x的方程![]() ,
,
化简为![]() ,
,
令![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() 或1,
或1,
令![]() ,得
,得![]() ,
,
![]() 函数
函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() 关于x的方程
关于x的方程![]() 在
在![]() 上恰有1个实数根,
上恰有1个实数根,
则只需![]()
得![]() .
.
(3)由(1)知,当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,令
时,令![]() ,则
,则![]() 成立,
成立,
即![]() 成立
成立
将n依次取1,2,3,4,5,…………![]() ,
,
可得![]() ,
,
![]() ,
,
……
![]() ,
,
![]() ,
,
累加求和得:![]() ,
,
即当![]() 时,
时,![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】现有![]() ,
,![]() ,…,
,…,![]() 这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计
这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计![]() ,
,![]() ,
,![]() ,
,![]() 这4个球队已经赛过的场数分别为:
这4个球队已经赛过的场数分别为:![]() 队4场,
队4场,![]() 队3场,
队3场, ![]() 队2场,
队2场,![]() 队1场,则
队1场,则![]() 队比赛过的场数为( )
队比赛过的场数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“十三五”规划确定了到2020年消除贫困的宏伟目标,打响了精准扶贫的攻坚战,为完成脱贫任务,某单位在甲地成立了一家医疗器械公司吸纳附近贫困村民就工,已知该公司生产某种型号医疗器械的月固定成本为20万元,每生产1千件需另投入5.4万元,设该公司一月内生产该型号医疗器械x千件且能全部销售完,每千件的销售收入为![]() 万元,已知
万元,已知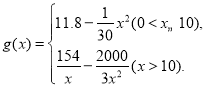
(1)请写出月利润y(万元)关于月产量x(千件)的函数解析式;
(2)月产量为多少千件时,该公司在这一型号医疗器械的生产中所获月利润最大?并求出最大月利润(精确到0.1万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自古以来“民以食为天”,餐饮业作为我国第三产业中的一个支柱产业,一直在社会发展与人民生活中发挥着重要作用.某机构统计了2010~2016年餐饮收入的情况,得到下面的条形图,则下面结论中不正确的是( )

A. 2010~2016年全国餐饮收入逐年增加
B. 2016年全国餐饮收入比2010年翻了一番以上
C. 2010~2016年全国餐饮收入同比增量最多的是2015年
D. 2010~2016年全国餐饮收入同比增量超过3000亿元的年份有3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com