
【题目】若函数f(x)=xln(x+ ![]() )为偶函数,则a= .
)为偶函数,则a= .
科目:高中数学 来源: 题型:
【题目】刘徽是我国魏晋时期著名的数学家,他编著的《海岛算经》中有一问题:“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高几何?” 意思是:为了测量海岛高度,立了两根表,高均为5步,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人恰观测到岛峰,从后表退行127步,也恰观测到岛峰,则岛峰的高度为( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题:
①函数y=tanx的一个对称中心是( ![]() ,0);
,0);
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一条对称轴是x=﹣
)的一条对称轴是x=﹣ ![]() ;
;
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数.
]上是增函数.
写出所有正确的命题的题号 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是为求S=1+ ![]() +
+ ![]() +…
+… ![]() 的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.
的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.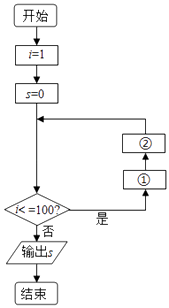
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() ,直线
,直线![]() 的极坐标方程分别是
的极坐标方程分别是![]() ,
, ![]() .
.
(1)求![]() 与
与![]() 的交点的极坐标;
的交点的极坐标;
(2)设![]() 为
为![]() 的圆心,
的圆心, ![]() 为
为![]() 与
与![]() 的交点连线的中点,已知直线
的交点连线的中点,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),求
为参数),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知θ为向量 ![]() 与
与 ![]() 的夹角,|
的夹角,| ![]() |=2,|
|=2,| ![]() |=1,关于x的一元二次方程x2﹣|
|=1,关于x的一元二次方程x2﹣| ![]() |x+
|x+ ![]()
![]() =0有实根.
=0有实根.
(Ⅰ)求θ的取值范围;
(Ⅱ)在(Ⅰ)的条件下,求函数f(θ)=sin(2θ+ ![]() )的最值及对应的θ的值.
)的最值及对应的θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 上的动点,
上的动点, ![]() .
.
(Ⅰ)若点![]() 是
是![]() 中点,证明:平面
中点,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)判断点![]() 到平面
到平面![]() 的距离是否为定值?若是,求出定值;若不是,请说明理由.
的距离是否为定值?若是,求出定值;若不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com