
已知函数g(x)=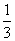 ax3+2x2-2x,函数f(x)是函数
ax3+2x2-2x,函数f(x)是函数 g(x)的导函数.
g(x)的导函数.
(1)若a=1,求g(x)的单调减区间;
(2)若对任意x1,x2∈R且x1≠x2,都有f ,求实数a的取值范围.
,求实数a的取值范围.
科目:高中数学 来源: 题型:
设函数f(x)=4sin(2x+1)-x,则在下列区间中函数f(x)不存在零点的是( )
A.[-4,-2] B.[-2,0]
C.[0,2] D.[2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的底面直径与高的比为( )
A.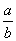 B.
B.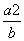 C.
C.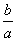 D.
D.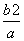
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)=x2-2x-3,x∈[0, m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( )
m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( )
A.(0,1] B.[1,2]
C.[2,+∞) D.(0,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
给出如下图所示程序,如果x1=2,x2=3,那么执行此程序的结果是输出( )
|

A.7 B.10 C.5 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com