
| A. | |$\overrightarrow{OA}$|+|$\overrightarrow{OB}$|>|$\overrightarrow{OA}$-$\overrightarrow{OB}$| | B. | |$\overrightarrow{AB}$|<$\sqrt{2}$ | C. | |$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$| | D. | ($\overrightarrow{OA}$+$\overrightarrow{OB}$)⊥($\overrightarrow{OA}$-$\overrightarrow{OB}$) |
分析 以OA,OB为邻边作平行四边形OACB,利用平面向量线性运算的几何意义和三角形,菱形知识进行判断.
解答 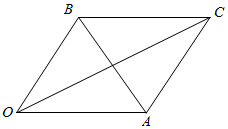 解:以OA,OB为邻边作平行四边形OACB则AB=|$\overrightarrow{OA}-\overrightarrow{OB}$|,
解:以OA,OB为邻边作平行四边形OACB则AB=|$\overrightarrow{OA}-\overrightarrow{OB}$|,
∵OA+OB>AB,∴|$\overrightarrow{OA}$|+|$\overrightarrow{OB}$|>|$\overrightarrow{OA}$-$\overrightarrow{OB}$|,故A正确.
∵OA=OB=1,∠AOB<90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}-2OA•OB•cos∠AOB}$=$\sqrt{2-2cos∠AOB}$$<\sqrt{2}$,故B正确.
∵|$\overrightarrow{OA}$+$\overrightarrow{OB}$|2=${\overrightarrow{OA}}^{2}$+${\overrightarrow{OB}}^{2}$+2$\overrightarrow{OA}•\overrightarrow{OB}$,|$\overrightarrow{OA}$-$\overrightarrow{OB}$|2=${\overrightarrow{OA}}^{2}$+${\overrightarrow{OB}}^{2}$-2$\overrightarrow{OA}•\overrightarrow{OB}$,
$\overrightarrow{OA}•\overrightarrow{OB}≠0$,
∴|$\overrightarrow{OA}$+$\overrightarrow{OB}$|≠|$\overrightarrow{OA}$-$\overrightarrow{OB}$|.故C错误.
∵OA=OB,∴四边形ABCD是菱形,
∴OC⊥AB,即($\overrightarrow{OA}$+$\overrightarrow{OB}$)⊥($\overrightarrow{OA}$-$\overrightarrow{OB}$),故D正确.
故选:C.
点评 本题考查了平面向量线性运算的几何意义,属于基础题.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{12\sqrt{13}}{13}$ | D. | $\frac{28\sqrt{13}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ | B. | -λ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x0∈R,sin2x0≥1 | B. | ¬p:?x∈R,sin2x≥1 | ||
| C. | ¬p:?x0∈R,sin2x0>1 | D. | ¬p:?x∈R,sin2x>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com