
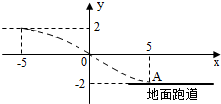
 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )
如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
| 3 |
| 125 |
| 3 |
| 5 |
| 6 |
| 125 |
| 4 |
| 5 |
| 9 |
| 125 |
| 9 |
| 125 |
| 1 |
| 5 |


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| 2 |
A、[
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、[-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 年龄(岁) | 工人数(人) |
| 19 | 1 |
| 28 | 3 |
| 29 | 3 |
| 30 | 5 |
| 31 | 4 |
| 32 | 3 |
| 40 | 1 |
| 合计 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com