
| 年龄(岁) | 工人数(人) |
| 19 | 1 |
| 28 | 3 |
| 29 | 3 |
| 30 | 5 |
| 31 | 4 |
| 32 | 3 |
| 40 | 1 |
| 合计 | 20 |

| 19+28×3+29×3+30×5+31×4+32×3+40 |
| 20 |
| 1 |
| 20 |


科目:高中数学 来源: 题型:
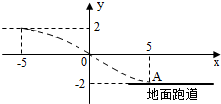 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )
如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、?x0∈R,x02+1>0 |
| B、?x0∈R,x02+1≤0 |
| C、?x0∈R,x02+1<0 |
| D、?x∈R,x2+1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为
乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| α |
| 2 |
| ||
| 4 |
| π |
| 6 |
| 2π |
| 3 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 |
| b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com