
已知点G是△ABC的重心,A(0, -1),B(0, 1),在x轴上有一点M,满足|![]() |=|
|=|![]() |,
|,![]() (
(![]() ∈R).
∈R).
⑴求点C的轨迹方程;
⑵若斜率为k的直线l与点C的轨迹交于不同两点P,Q,且满足|![]() |=|
|=|![]() |,试求k的取值范围.
|,试求k的取值范围.
⑴设C(x, y),则G(![]() ,
,![]() ).∵
).∵![]() (
(![]() ∈R),∴GM//AB,
∈R),∴GM//AB,
又M是x轴上一点,则M(![]() , 0).又|
, 0).又|![]() |=|
|=|![]() |,
|,
∴![]() ,
,
整理得![]() ,即为曲线C的方程.
,即为曲线C的方程.
⑵①当k=0时,l和椭圆C有不同两交点P,Q,根据椭圆对称性有|![]() |=|
|=|![]() |.
|.
②当k≠0时,可设l的方程为y=kx+m,
![]() 联立方程组 y=kx+m
联立方程组 y=kx+m
![]()
消去y,整理行(1+3k2)x2+6kmx+3(m2-1)=0(*)
∵直线l和椭圆C交于不同两点,
∴△=(6km)2-4(1+3k2)×( m2-1)>0,即1+3k2-m2>0. (1)
设P(x1, y1),Q(x2, y2),则x1, x2是方程(*)的两相异实根,∴x1+x2=-![]()
则PQ的中点N(x0, y0)的坐标是x0=![]() =-
=-![]() ,y0= k x0+m=
,y0= k x0+m=![]() ,
,
即N(-![]() ,
, ![]() ),
),
又|![]() |=|
|=|![]() |,∴
|,∴![]() ⊥
⊥![]() ,
,
∴k·kAN=k·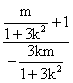 =-1,∴m=
=-1,∴m=![]() .
.
将m=![]() 代入(1)式,得 1+3k2-(
代入(1)式,得 1+3k2-(![]() )2>0(k≠0),
)2>0(k≠0),
即k2<1,∴k∈(-1, 0)∪(0, 1).
综合①②得,k的取值范围是(-1, 1).
本题依托向量给出等量关系,既考查向量的模、共线等基础知识,又考查动点的轨迹,直线与椭圆的位置关系.通过向量和解析几何间的联系,陈题新组,考查基础知识和基本方法.按照求轨迹方程的方法步骤,把向量问题坐标化,几何问题代数化. 对题目的要求:有较大的难度,有特别的解题思路、演变角度,要有一定的梯度.


科目:高中数学 来源: 题型:
| MA |
| MC |
| GM |
| AB |
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AP |
| AB |
| AC |
A、(
| ||
B、(
| ||
C、(1,
| ||
| D、(1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| OA |
| OB |
| OC |
| OG |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 5 |
| AM |
| AB |
| AN |
| AC |
| 1 |
| x |
| 1 |
| y |
| ∫ | π 0 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com