
分析 (Ⅰ)根据ρ2=x2+y2,ρcosθ=x,ρsinθ=y,求出C的直角坐标方程,通过配方求出圆心和半径即可;
(Ⅱ)求出直线过定点M(5,0),设出直线方程,根据|PQ|=4,求出直线方程即可.
解答 解:( I)由ρ=4cosθ-2sinθ,
得ρ2=4ρcosθ-2ρsinθ,
将ρ2=x2+y2,ρcosθ=x,ρsinθ=y,
代入可得x2+y2-4x+2y=0,
配方,得(x-2)2+(y+1)2=5,
所以圆心为(2,-1),半径为$\sqrt{5}$.
( II)由直线L的参数方程知直线过定点M(5,0),
则由题意,知直线l的斜率一定存在,
因此不妨设直线l的方程为l的方程为y=k(x-5),
因为|PQ|=4,所以5-${(\frac{|1-3k|}{\sqrt{{k}^{2}+1}})}^{2}$=4,
解得k=0或k=$\frac{3}{4}$.
点评 本题考查了极坐标方程转化为直角坐标方程,考查求直线方程问题,是一道中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
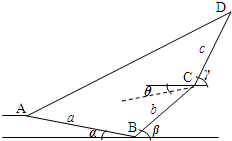 某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面
某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com