
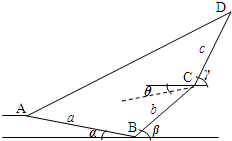
 某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面
某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面分析 (1)分别过点C,D作CE⊥BE,DF⊥CF,垂足分别为E,F,解三角形可得,
(2)根据余弦定理即可求出.
解答 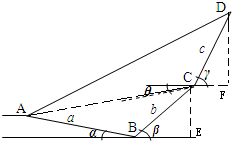 解:(1)分别过点C,D作CE⊥BE,DF⊥CF,垂足分别为E,F,
解:(1)分别过点C,D作CE⊥BE,DF⊥CF,垂足分别为E,F,
在Rt△CBF和Rt△DCF中,CF=bsinβ,DF=csin γ
∴h=CF+DF=bsin β+csin γ.
(2):联结AC.在△ABC中,由余弦定理得AC2=a2+b2+2abcos(α+β),
在△ACD中,由余弦定理得AD2=AC2+c2-2cACcos(π-γ+θ),
所以AD=α$\sqrt{{a}^{2}+{b}^{2}+2abcos(α+β)+{c}^{2}+2c\sqrt{{a}^{2}+{b}^{2}+2abcos(α+β)}cos(γ-θ)}$.
点评 本题考查了解三角形实际生活中的应用,关键是构造三角形,利用余弦定理,属于基础题.


科目:高中数学 来源: 题型:解答题
 一次考试中,五名学生的数学、物理成绩如表所示:
一次考试中,五名学生的数学、物理成绩如表所示:| 学生 | A | B | C | D | E |
| 数学成绩x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理成绩y(分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com