
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(0,3) | B. | (-3,0)∪(3,+∞) | C. | (-∞,-3)∪(-3,0) | D. | (0,3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 3 | D. | 3-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
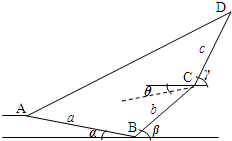 某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面
某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z=$\frac{1}{5}$x-y | B. | z=-3x+y | C. | z=$\frac{1}{5}$x+y | D. | z=3x-y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x-1与g(x)=$\sqrt{{{(x-1)}^2}}$ | B. | f(x)=x与g(x)=${(\sqrt{x})^2}$ | ||
| C. | f(x)=x2-x与g(t)=t2-t | D. | f(x)=x-1与g(x)=$\frac{{{x^2}-1}}{x+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com