
 一次考试中,五名学生的数学、物理成绩如表所示:
一次考试中,五名学生的数学、物理成绩如表所示:| 学生 | A | B | C | D | E |
| 数学成绩x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理成绩y(分) | 87 | 89 | 89 | 92 | 93 |
分析 (1)根据所给的数据先做出数据的平均数,即样本中心点,根据最小二乘法做出线性回归方程的系数,写出线性回归方程;
(2)用列举法可得从5名学生中任取2名学生的所有情况和其中至少有一人物理成绩高于90分的情况包含的事件数目,由古典概型公式,计算可得答案.
解答 解:(1)∵$\overline x$=93,$\overline y$=90,$\sum_{i=1}^5{{{({x_i}-\overline x)}^2}}$=40,$\sum_{i=1}^5$(xi-$\overline x$)(yi-$\overline y$)=30,
∴$\widehatb$=0.75,$\widehata$=20.25,
故y关于x的线性回归方程是:$\widehaty$=0.75x+20.25.
(2)从5名学生中任取2名学生的所有情况为:(A4,A5)、(A4,A1)、(A4,A2)、(A4,A3)、(A5,A1)、(A5,A2)、(A5,A3)、(A1,A2)、(A1,A3)、(A2,A3)共种情10况.…(3分)
其中至少有一人物理成绩高于90分的情况有:(A4,A5)、(A4,A1)、(A4,A2)、(A4,A3)、(A5,A1)、(A5,A2)、(A5,A3)共7种情况,
故上述抽取的5人中选2人,选中的学生的物理成绩至少有一人的成绩高于90分的概率P=0.7.
点评 本题主要考查了古典概型和线性回归方程等知识,考查了学生的数据处理能力和应用意识.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
| 正误 年龄 | 正确 | 错误 | 合计 |
| [20,30) | 10 | 30 | 40 |
| [30,40] | 10 | 70 | 80 |
| 合计 | 20 | 100 | 120 |
| P(K2<k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(0,3) | B. | (-3,0)∪(3,+∞) | C. | (-∞,-3)∪(-3,0) | D. | (0,3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{{\sqrt{3}}}{2}$,$\sqrt{3}}$] | B. | ($\frac{\sqrt{3}}{2}$,$\sqrt{3}$) | C. | ($\frac{\sqrt{3}}{3}$,$\sqrt{3}$] | D. | ($\frac{\sqrt{3}}{3}$,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±2\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $±\sqrt{15}$ | D. | $4\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
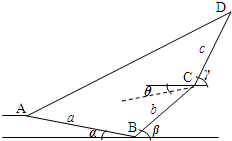 某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面
某旅游景点有一处山峰,游客需从景点入口A处向下沿坡角为α的一条小路行进a百米后到达山脚B处,然后沿坡角为β的山路向上行进b百米后到达山腰C处,这时回头望向景点入口A处俯角为θ,由于山势变陡到达山峰D坡角为γ,然后继续向上行进c百米终于到达山峰D处,游览风景后,此游客打算乘坐由山峰D直达入口A的缆车下山结束行程,如图,假设A、B、C、D四个点在同一竖直平面查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com