
| 正误 年龄 | 正确 | 错误 | 合计 |
| [20,30) | 10 | 30 | 40 |
| [30,40] | 10 | 70 | 80 |
| 合计 | 20 | 100 | 120 |
| P(K2<k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
分析 (Ⅰ)根据所给的二维条形图得到列联表,利用公式求出k2=3>2.706,即可得出结论;
(Ⅱ)设事件A为3名幸运选手中至少有一人在20~30岁之间,由已知得20~30岁之间的人数为2人,30~40岁之间的人数为4人,从6人中取3人的结果有15种,事件A的结果有8种,即可求出两名幸运选手不在同一年龄段的概率.
解答 解:(Ⅰ)由k=$\frac{120×(70×10-30×10)^{2}}{20×100×40×80}$=3>2.706
所以有90%的把握认为猜对歌曲名称与否和年龄有关.
(Ⅱ)设事件A为两名幸运选手不在同一年龄段,由已知得20~30岁之间的人数为2人,30~40岁之间的人数为4人,
从6人中取2人的结果有15种,事件A的结果有8种,
故两名幸运选手不在同一年龄段的概率P(A)=$\frac{8}{15}$.
点评 本题考查独立性检验知识的运用,考查分层抽样,考查概率知识,考查学生分析解决问题的能力,确定基本事件总数是关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
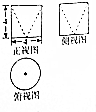
| A. | 24π+4$\sqrt{5}$π | B. | 20π+4$\sqrt{5}$π | C. | 24π+8$\sqrt{5}$π | D. | 20π+8$\sqrt{5}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7,-20 | B. | 0,-9 | C. | -9,-20 | D. | -4,-20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 10 | C. | 7 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
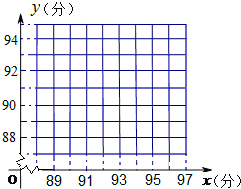 一次考试中,五名学生的数学、物理成绩如表所示:
一次考试中,五名学生的数学、物理成绩如表所示:| 学生 | A | B | C | D | E |
| 数学成绩x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理成绩y(分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com